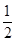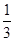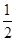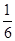题目内容
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:| 甲 | 乙 | ||||||||||||||||||
| 环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 | ||||||||||||
| 概率 |
|
|
|
概率 |
|
|
| ||||||||||||
(2)若两个射手各射击1次,记所得的环数之和为ξ,求ξ的分布列和期望.
分析:(1)若甲乙两射手各射击两次,四次射击中恰有三次命中10环分两类:甲命中1次10环,乙命中两次10环和甲命中2次10环,乙命中1次10环,分别求概率再求和;
(2)ξ的取值分别为16,17,18,19,20,利用独立事件的概率求法分别求ξ取每个值的概率即可.
(2)ξ的取值分别为16,17,18,19,20,利用独立事件的概率求法分别求ξ取每个值的概率即可.
解答:解(Ⅰ)记事件C;甲命中1次10环,乙命中两次10环,事件D;甲命中2次10环,乙命中1次10环,则四次射击中恰有三次命中10环为事件C+D∴P(C+D)=
×
×
×
(
)2+
(
)2×
×
=
(Ⅱ)ξ的取值分别为16,17,18,19,20,
P(ξ=16)=
×
=
,P(ξ=17)=
×
+
×
=
P(ξ=18)=
×
+
×
+
×
=
=
,
P(ξ=19)=
×
+
×
=
=
,P(ξ=20)=
×
=
∴Eξ=16×
+17×
+18×
+19×
+20×
=
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 2 2 |
| 1 |
| 6 |
| C | 2 2 |
| 1 |
| 3 |
| 5 |
| 6 |
| 1 |
| 6 |
| 7 |
| 162 |
(Ⅱ)ξ的取值分别为16,17,18,19,20,
P(ξ=16)=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 18 |
P(ξ=18)=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 6 |
| 18 |
| 1 |
| 3 |
P(ξ=19)=
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 18 |
| 2 |
| 9 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 18 |
∴Eξ=16×
| 1 |
| 9 |
| 5 |
| 18 |
| 1 |
| 3 |
| 2 |
| 9 |
| 1 |
| 18 |
| 107 |
| 6 |
点评:本题考查独立事件、互斥事件的概率、离散型随机变量的分布列、期望等知识,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(12分)甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
射手甲 |
| 射手乙 | ||||||
环数 | 8 | 9 | 10 | 环数 | 8 | 9 | 10 | |
概率 |
|
|
| 概率 |
|
|
| |
(I)若甲射手共有5发子弹,一旦命中10环就停止射击,求他剩余3颗子弹的概率;
(Ⅱ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅲ)若两个射手各射击1次,记所得的环数之和为![]() ,求
,求![]() 的分布列和期望。
的分布列和期望。
(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
|
射手甲 |
射手乙 |
||||||
|
环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
|
概率 |
|
|
|
概率 |
|
|
|
(Ⅰ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅱ)若两个射手各射击1次,记所得的环数之和为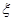 ,求
,求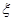 的分布列和期望.
的分布列和期望.
(本小题满分13分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:K^S*5U.C#O%
|
射手甲 |
射手乙 |
||||||
|
环数 |
8 |
9 |
10 |
环数 |
8 |
9 |
10 |
|
概率 |
|
|
|
概率 |
|
|
|
(1)若甲射手共有5发子弹,一旦命中10环就停止射击,求他剩余3颗子弹的概率;
(2)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;K^S*5U.C#O%
(3)若两个射手各射击1次,记所得的环数之和为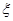 ,求
,求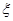 的分布列和期望。
的分布列和期望。