题目内容
圆锥的轴截面是等腰直角三角形,如图所示,底面圆的半径为1,点O是圆心,过顶点S的截面SAB与底面所成的二面角是60°(1)求截面SAB的面积;
(2)求点O到截面SAB的距离.
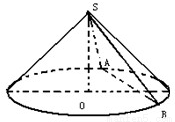
【答案】分析:(1)取AB中点C,连接OC,SC,则∠SCO=60°,SO=1,所以OC=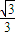 ,SC=
,SC= ,AB=
,AB=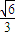 ,由此能求出截面SAB的面积.
,由此能求出截面SAB的面积.
(2)在Rt△SOC中,作OD⊥SC,则OD即为所求.
解答: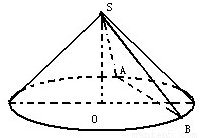 解:(1)取AB中点C,
解:(1)取AB中点C,
连接OC,SC,
则∠SCO=60°
SO=1,
所以OC=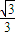 ,SC=
,SC=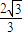 ,AB=
,AB=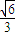 ,
,
∴截面SAB的面积S= .
.
(2)在Rt△SOC中,
作OD⊥SC,
则OD即为所求,
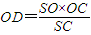 =
=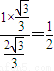 .
.
点评:本题考查截面SAB的面积和点O到截面SAB的距离的求法.解题时要认真审题,仔细观察,注意合理地进行等价转化,把立体几何问题转化为平面几何问题进行求解.
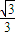 ,SC=
,SC= ,AB=
,AB=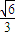 ,由此能求出截面SAB的面积.
,由此能求出截面SAB的面积.(2)在Rt△SOC中,作OD⊥SC,则OD即为所求.
解答:
 解:(1)取AB中点C,
解:(1)取AB中点C,连接OC,SC,
则∠SCO=60°
SO=1,
所以OC=
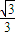 ,SC=
,SC=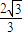 ,AB=
,AB=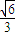 ,
,∴截面SAB的面积S=
 .
.(2)在Rt△SOC中,
作OD⊥SC,
则OD即为所求,
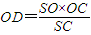 =
=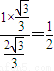 .
.点评:本题考查截面SAB的面积和点O到截面SAB的距离的求法.解题时要认真审题,仔细观察,注意合理地进行等价转化,把立体几何问题转化为平面几何问题进行求解.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 求答下列三小题:
求答下列三小题: (2009•南汇区二模)圆锥的轴截面是等腰直角三角形,如图所示,底面圆的半径为1,点O是圆心,过顶点S的截面SAB与底面所成的二面角是60°
(2009•南汇区二模)圆锥的轴截面是等腰直角三角形,如图所示,底面圆的半径为1,点O是圆心,过顶点S的截面SAB与底面所成的二面角是60°