Question

双曲线C：=1(a＞0,b＞0)的离心率为2，焦点到双曲线C的渐近线的距离为.点P的坐标为(0，-2)，过P的直线l与双曲线C交于不同的两点M、N.

(1)若PM=2PN,求直线l的方程；

(2)设O为坐标原点，求的取值范围.

Answer 1

解：双曲线C的渐近线为bx±ay=0，焦点(c，0)到渐近线的距离d=，得b=．又=2，即a²+b²=4a²，解得a²=4.

∴双曲线C的方程为=1.                                              

设M(x₁,y₁),N(x₂,y₂).

(1)由，得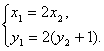

又M、N在双曲线上，

∴

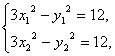
解得y₂=4,x₂=±.

∴直线l的斜率k=.                                        

∴直线l的方程为y=±x-2.                                               

(2)由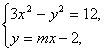得(3-m²)x²+4mx-16=0，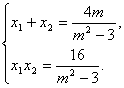                   

=(x₁,y₁)·(x₂,y₂)

=(x₁,mx₁-2)·(x₂,mx₂-2)

=(m²+1)x₁x₂-2m(x₁+x₂)+4

=12+.                                                              

又∵Δ=16m²-4(3-m²)(-16)＞0，且3-m≠0，∴-2＜m＜2且m≠±.                 

∴＞52或≤.