题目内容
设r>0,两圆(x-1)2+(y+3)2=r2与x2+y2=16可能
- A.相离
- B.相交
- C.内切或内含或相交
- D.外切或外离
C
分析:先计算两圆的圆心距,再与半径的和差比较,可判断.
解答:∵两圆圆心坐标为(1,-3),(0,0)
∴两圆的圆心距的平方为(0-1)2+(0+3)2=10,半径分别为4,r,
∴当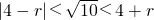 时,两圆相交;当
时,两圆相交;当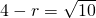 时,两圆内切;当
时,两圆内切;当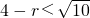 时,两圆内含.
时,两圆内含.
故选C.
点评:本题主要考查圆与圆的位置关系,利用代数方法可解.
分析:先计算两圆的圆心距,再与半径的和差比较,可判断.
解答:∵两圆圆心坐标为(1,-3),(0,0)
∴两圆的圆心距的平方为(0-1)2+(0+3)2=10,半径分别为4,r,
∴当
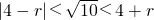 时,两圆相交;当
时,两圆相交;当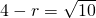 时,两圆内切;当
时,两圆内切;当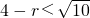 时,两圆内含.
时,两圆内含.故选C.
点评:本题主要考查圆与圆的位置关系,利用代数方法可解.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
设r>0,两圆(x-1)2+(y+3)2=r2与x2+y2=16可能( )
| A、相离 | B、相交 | C、内切或内含或相交 | D、外切或外离 |