题目内容
若(x3+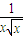 )n的展开式中的常数项为84,则n= .
)n的展开式中的常数项为84,则n= .
【答案】分析:利用二项展开式的通项公式求出第r+1项,令x的指数为0求出常数项列出方程求出n,r的关系,进而可得答案.
解答:解:Tr+1=Cnr(x3)n-r =
=
令3n- r=0,
r=0,
∴2n=3r.
∴n必为3的倍数,r为偶数.
试验可知n=9,r=6时,Cnr=C96=84.
故答案为9
点评:本题考查二项展开式的通项公式是解决二项展开式的特点项问题的工具.
解答:解:Tr+1=Cnr(x3)n-r
 =
=
令3n-
 r=0,
r=0,∴2n=3r.
∴n必为3的倍数,r为偶数.
试验可知n=9,r=6时,Cnr=C96=84.
故答案为9
点评:本题考查二项展开式的通项公式是解决二项展开式的特点项问题的工具.

练习册系列答案
相关题目
 )n的展开式中的常数项为84,则n= .
)n的展开式中的常数项为84,则n= .