题目内容
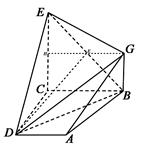
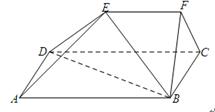
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且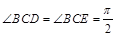 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
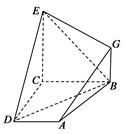
(1)求证: EC⊥CD;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
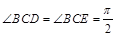 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
(1)求证: EC⊥CD;
(2)求证:AG∥平面BDE;
(3)求:几何体EG-ABCD的体积.
(1)证明过程详见解析;(2)证明过程详见解析;(3)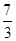
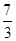
试题分析:(1)要证
 ,只要证
,只要证 平面
平面 ;而由题设平面
;而由题设平面 平面
平面 且
且 ,所以
,所以 平面
平面 ,结论得证;
,结论得证;(2)过G作GN⊥CE交BE于M,连 DM,由题设可证四边形
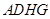 为平行四边形,所以有
为平行四边形,所以有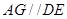
从而由直线与平面平行的判定定理,可证AG∥平面BDE;
(3)欲求几何体EG-ABCD的体积,可先将该几何体分成一个四棱锥
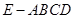 和三棱锥
和三棱锥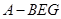 .
.试题解析:
(1)证明:由平面ABCD⊥平面BCEG,
平面ABCD∩平面BCEG=BC,
 平面BCEG,
平面BCEG,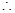 EC⊥平面ABCD,3分
EC⊥平面ABCD,3分又CD
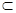 平面BCDA, 故 EC⊥CD4分
平面BCDA, 故 EC⊥CD4分(2)证明:在平面BCDG中,过G作GN⊥CE交BE于M,连DM,则由已知知;MG=MN,MN∥BC∥DA,且
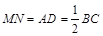
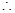 MG∥AD,MG=AD, 故四边形ADMG为平行四边形,
MG∥AD,MG=AD, 故四边形ADMG为平行四边形,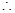 AG∥DM6分
AG∥DM6分∵DM
 平面BDE,AG
平面BDE,AG 平面BDE,
平面BDE, 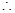 AG∥平面BDE8分
AG∥平面BDE8分(3)解:
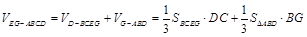 10分
10分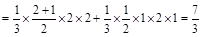 12分
12分
练习册系列答案
相关题目
 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形,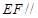 平面
平面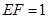 ,
,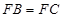 ,
,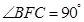 ,
,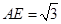 .
.
 平面
平面 ;
; 与平面
与平面 所成角的正切值.
所成角的正切值.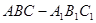 中,四边形
中,四边形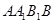 是菱形,四边形
是菱形,四边形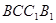 是矩形,
是矩形, .
.
 ;
; 到平面
到平面 的距离;
的距离; 与平面
与平面 是两条不同的直线,
是两条不同的直线,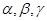 是三个不同的平面,则下列命题正确的是( )
是三个不同的平面,则下列命题正确的是( )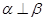 ,
,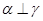 ,则
,则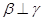
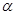 所成的角相等,则
所成的角相等,则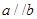
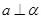 ,
,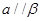 ,则
,则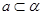 ,则
,则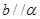
 //平面
//平面 ,直线
,直线 平面
平面
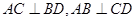 ,则
,则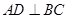 ;
;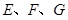 分别是
分别是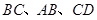 的中点,则
的中点,则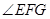 的大小等于异面直线
的大小等于异面直线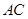 与
与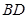 所成角的大小;
所成角的大小;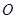 是四面体
是四面体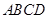 外接球的球心,则
外接球的球心,则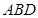 上的射影为
上的射影为 的外心;
的外心;