题目内容
函数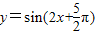
的一个对称中心是（ ）A．
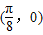
B．
C．
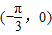
D．
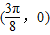
【答案】分析：利用诱导公式对函数化简可得，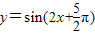
=cos2x根据余弦函数的对称中心可令2x=kπ+
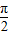，可求函数的对称中心为，结合选项找出正确答案即可
解答：解：∵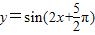
=cos2x
令2x=kπ+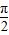
可得
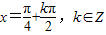
函数的对称中心为：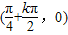
，结合选项可知当k=0时，选项B正确
故选B
点评：形如y=Asin（ωx+φ）型的函数的对称轴（对称中心）的求解一般是根据正弦函数的性质，整体求解：令ωx+φ分别满足正弦函数的对称轴（对称中心）的值，然后解x的值．
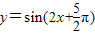=cos2x根据余弦函数的对称中心可令2x=kπ+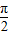，可求函数的对称中心为，结合选项找出正确答案即可解答：解：∵
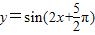=cos2x令2x=kπ+
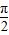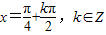
可得函数的对称中心为：
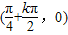，结合选项可知当k=0时，选项B正确故选B
点评：形如y=Asin（ωx+φ）型的函数的对称轴（对称中心）的求解一般是根据正弦函数的性质，整体求解：令ωx+φ分别满足正弦函数的对称轴（对称中心）的值，然后解x的值．
练习册系列答案
相关题目
将函数y=sin（6x+
）的图象上各点的横坐标伸长到原来的3倍，再向右平移
个单位，得到的函数的一个对称中心是（ ）
| π |
| 4 |
| π |
| 8 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
的图像上各点的横坐标伸长到原来的3倍，再向右平移
个单位，得到的函数的一个对称中心是 （ ）
B．
C．
D．
的图象上各点的横坐标伸长到原来的3倍，再向右平移
个单位，得到的函数的一个对称中心是（ ）
B．
C．
D．