题目内容
已知n为正偶数，用数学归纳法证明
时，
若已假设
为偶数）时命题为真，则还需要用归纳假设再证
A．
时等式成立 B．
时等式成立
C．
时等式成立 D．
时等式成立
【答案】
B
【解析】略
练习册系列答案
53随堂测系列答案
相关题目
已知n为正偶数，用数学归纳法证明1-
+
-
+…+
-
=2(
+
+…+
)时，若已假设n=k（k≥2，k为偶数）时命题为真，则还需要用归纳假设再证n= 时等式成立．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| n+4 |
| 1 |
| 2n |
已知n为正偶数，用数学归纳法证明1-
+
-
+…+
=2（
+
+…+
）时，若已假设n=k（k≥2为偶数）时命题为真，则还需要用归纳假设再证（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n+2 |
| 1 |
| n+4 |
| 1 |
| 2n |
| A、n=k+1时等式成立 |
| B、n=k+2时等式成立 |
| C、n=2k+2时等式成立 |
| D、n=2（k+2）时等式成立 |
时，若已假设
为偶数）时命题为真，则还需要用归纳假设再证
（ ）时等式成立 （ ）
B．
C．
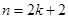D．