题目内容
已知n为正偶数,用数学归纳法证明1-
+
-
+…+
=2(
+
+…+
)时,若已假设n=k(k≥2)为偶数)时命题为真,则还需要用归纳假设再证n=( )时等式成立.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+4 |
| 1 |
| 2n |
分析:直接利用数学归纳法的证明方法,判断选项即可.
解答:解:由数学归纳法的证明步骤可知,假设n=k(k≥2)为偶数)时命题为真,
则还需要用归纳假设再证n=k+2,
不是n=k+1,因为n是偶数,k+1是奇数,
故选B.
则还需要用归纳假设再证n=k+2,
不是n=k+1,因为n是偶数,k+1是奇数,
故选B.
点评:本题考查数学归纳法的证明方法的应用,基本知识的考查.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知n为正偶数,用数学归纳法证明1-
+
-
+…+
-
=2(
+
+…+
)时,若已假设n=k(k≥2,k为偶数)时命题为真,则还需要用归纳假设再证n= 时等式成立.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| n+4 |
| 1 |
| 2n |
已知n为正偶数,用数学归纳法证明1-
+
-
+…+
=2(
+
+…+
)时,若已假设n=k(k≥2为偶数)时命题为真,则还需要用归纳假设再证( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n+2 |
| 1 |
| n+4 |
| 1 |
| 2n |
| A、n=k+1时等式成立 |
| B、n=k+2时等式成立 |
| C、n=2k+2时等式成立 |
| D、n=2(k+2)时等式成立 |
 时,若已假设
时,若已假设 为偶数)时命题为真,则还需要用归纳假设再证
为偶数)时命题为真,则还需要用归纳假设再证 ( )时等式成立 ( )
( )时等式成立 ( ) B.
B. C.
C.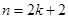 D.
D.
 时,
时, 为偶数)时命题为真,则还需要用归纳假设再证
为偶数)时命题为真,则还需要用归纳假设再证 时等式成立 B.
时等式成立 B. 时等式成立
时等式成立 时等式成立 D.
时等式成立 D. 时等式成立
时等式成立