题目内容
【题目】已知函数![]() .
.
(1)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)已知不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的最大值;
的最大值;
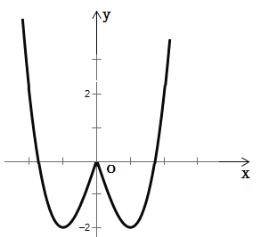
(3)当![]() 时,求函数
时,求函数![]() 的零点个数.
的零点个数.
【答案】(1)见解析(2)![]() (3)9个
(3)9个
【解析】
(1) 当![]() 时,
时,![]() 可得
可得![]() 是偶函数,当
是偶函数,当![]() 时,可得
时,可得![]() 是非奇非偶函数.
是非奇非偶函数.
(2) 当![]() 时,
时, ![]() ,即将问题转化为
,即将问题转化为![]() 在
在![]() 上恒成立,设
上恒成立,设![]() ,只要使
,只要使![]() .然后求出
.然后求出![]() 的导数,求出函数
的导数,求出函数![]() 的最小值.
的最小值.
(3)当![]() 时,
时,![]() ,得到
,得到![]() 得
得![]() 或
或![]() ,问题即求
,问题即求![]() 和
和![]() 和
和![]() 三个方程总的解的个数.
三个方程总的解的个数.
解:(1)函数定义域为![]() ,关于原点对称.
,关于原点对称.
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
则![]() 是定义在
是定义在![]() 上的偶函数;
上的偶函数;
当![]() 时,
时,![]() ,
,![]() ,
,
![]() 且
且![]() ,
,
所以![]() 是非奇非偶函数.
是非奇非偶函数.
(2)当![]() 时,
时,![]() ,即已知
,即已知![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,只要使
,只要使![]() .
.
![]() ,因为
,因为![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
即![]() 的最小值是
的最小值是![]() ,
,
解不等式![]() ,得
,得![]() .所以实数
.所以实数![]() 的最大值是
的最大值是![]() .
.
(3)当![]() 时,
时,![]() ,解
,解![]() 得
得![]() 或
或![]() ,
,
问题即求![]() 和
和![]() 和
和![]() 三个方程总的解的个数.
三个方程总的解的个数.
由(1)得函数![]() 是偶函数,
是偶函数,
当![]() 时,
时,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
所以![]() ,且
,且![]()
由偶函数的性质,![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
方程![]() 有3个解;方程
有3个解;方程![]() 有2个解;
有2个解;
方程![]() 有4个解;所以函数
有4个解;所以函数![]() 的零点个数是9个.
的零点个数是9个.

【题目】甲、乙两陶瓷厂生产规格为![]() 的矩形瓷砖(长和宽都约为
的矩形瓷砖(长和宽都约为![]() ) ,根据产品出厂检测结果,每片瓷砖质量
) ,根据产品出厂检测结果,每片瓷砖质量![]() (单位:
(单位:![]() )在
)在![]() 之间的称为正品,其余的作为废品直接回炉处理.正品瓷
之间的称为正品,其余的作为废品直接回炉处理.正品瓷
砖按行业生产标准分为“优等”、“一级”、“合格”三个标准,主要按照每片瓷砖的“尺寸误差”加以划分,每片价格分别为![]() 元、
元、![]() 元、
元、![]() 元.若规定每片正品瓷砖的“尺寸误差”计算方式为,设矩形瓷砖的长与宽分别为
元.若规定每片正品瓷砖的“尺寸误差”计算方式为,设矩形瓷砖的长与宽分别为![]() (单位:
(单位:![]() ) ,则“尺寸误差”为
) ,则“尺寸误差”为![]() ,“优等”瓷砖的“尺寸误差”范围是
,“优等”瓷砖的“尺寸误差”范围是![]() ,“一级”瓷砖的“尺寸误差”范围是
,“一级”瓷砖的“尺寸误差”范围是![]() ,“合格”瓷砖的“尺寸误差”范围是
,“合格”瓷砖的“尺寸误差”范围是![]() .现分别从甲、乙两厂生产的正品瓷砖中随机抽取
.现分别从甲、乙两厂生产的正品瓷砖中随机抽取![]() 片瓷砖,相应的“尺寸误差”组成的样本数据如下:
片瓷砖,相应的“尺寸误差”组成的样本数据如下:
(甲厂产品的“尺寸误差”频数表)
尺寸误差 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(乙厂产品的“尺寸误差”柱状图)

(1)根据样本数据分别计算甲、乙两厂生产的正品瓷砖的“尺寸误差”的平均值;
(2)若用这个样本的频率分布估计总体分布,求乙厂所生产的正品瓷砖的平均价格;
(3)现用分层抽样的方法从甲厂生产的![]() 片样本瓷砖中随机抽取
片样本瓷砖中随机抽取![]() 片,再从抽取的
片,再从抽取的![]() 片瓷砖中的“一级”瓷砖与“合格”瓷砖中随机选.取
片瓷砖中的“一级”瓷砖与“合格”瓷砖中随机选.取![]() 片进一步分析其“平整度”,求这
片进一步分析其“平整度”,求这![]() 片瓷砖的价格之和大于
片瓷砖的价格之和大于![]() 元的概率.
元的概率.


