题目内容
已知 l,m,n是互不相同的直线,α,β是不同的平面,则下列四个命题:
①m?α,l∩α=A,点A∉m,则 l与 m 是异面直线;
②若l∥α,m∥β,α∥β,则l∥m;
③l、m是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;
④若l?α,m?α,l∩m=A,l∥β,m∥β,则α∥β
其中是真命题的是 ______(请写出所有正确答案的序号)
①m?α,l∩α=A,点A∉m,则 l与 m 是异面直线;
②若l∥α,m∥β,α∥β,则l∥m;
③l、m是异面直线,l∥α,m∥α,且n⊥l,n⊥m,则n⊥α;
④若l?α,m?α,l∩m=A,l∥β,m∥β,则α∥β
其中是真命题的是 ______(请写出所有正确答案的序号)
因为平面α外的直线l经过平面α内的一点A,平面α内的直线m不过点A,故l与 m 是异面直线,故①正确.
由 l∥α,m∥β,α∥β,可得 l与 m 可能平行、可能相交,也可能是异面直线,故 ②不正确.
∵l、m是异面直线,l∥α,m∥α,且n⊥l,n⊥m,∴l、m在平面α内的射影是两条相交直线,
且n垂直于平面α内的这两条射影,故n⊥α成立,故③正确.
由于平面α内的两条相交的直线l和m都平行于平面β,由面面平行的判定定理知 α∥β.
综上,①③④正确,②不正确,
故答案为 ①③④.
由 l∥α,m∥β,α∥β,可得 l与 m 可能平行、可能相交,也可能是异面直线,故 ②不正确.
∵l、m是异面直线,l∥α,m∥α,且n⊥l,n⊥m,∴l、m在平面α内的射影是两条相交直线,
且n垂直于平面α内的这两条射影,故n⊥α成立,故③正确.
由于平面α内的两条相交的直线l和m都平行于平面β,由面面平行的判定定理知 α∥β.
综上,①③④正确,②不正确,
故答案为 ①③④.

练习册系列答案
相关题目
 α,a
α,a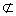 β,在α,β内的射影分别为直线b和c,则b,c的位置关系是( )。
β,在α,β内的射影分别为直线b和c,则b,c的位置关系是( )。