Question

已知A={x|x²-4x+3＜0，x∈R}，B={x|x²-2（a+7）x+5≤0，x∈R}，若A⊆B，则实数a的取值范围是

 

．

Answer 1

分析：先化简集合A={x|x²-4x+3＜0，x∈R}，B={x|x²-2（a+7）x+5≤0，x∈R}，再结合数轴表示利用题中条件：“A⊆B”列出不等关系，从而解决问题．

解答：解：∵A={x|x²-4x+3＜0，x∈R}={x|1＜x＜3}，
B集合表示不等式x²-2（a+7）x+5≤0的解集，

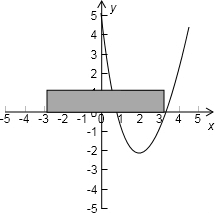
设f（x）=x²-2（a+7）x+5，画出图象．
若A⊆B，由图得：

f(1)≤0 f(3)≤0

即

1-2(a+7)+5≤0 9-2(a+7)×3+5≤0

解得：a≥-4
故答案为a≥-4．

点评：本题属于以一元二次函数为依托，求集合的包含关系的基础题，也是高考常会考的题型．