Question

【题目】已知函数，，

（1）当时，求函数的单调递增与单调递减区间（直接写结果）；

（2）当时，函数在区间上的最大值为，试求实数m的取值范围；

（3）若不等式对任意，恒成立，求实数b的取值范围.

Answer 1

【答案】（1）增区间为，减区间为；

（2）；

（3）.

【解析】

（1）将题中所给的的值代入解析式，利用对勾函数的性质写出函数的单调增区间和减区间即可；

（2）解不等式即可得结果；

（3）将题中所给的式子进行变形，将问题转化为在上单调递增，结合分段函数的解析式和二次函数图象的对称轴，分类讨论得到结果.

（1）当时，，

所以函数的单调增区间为和，

单调减区间为和；

（2）因为，

且函数在上单调递减，在上单调递增，

又因为在上的最大值为，所以，

即，整理得，

所以，所以，即，

所以的取值范围是；

（3）由对任意恒成立，

即，

令，等价于在上单调递增，

而，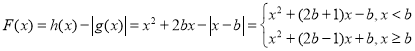

分以下三种情况来讨论：

（i）当时，即时，

结合函数图象可得，解得，矛盾，无解；

（ii）时，即时，

函数图象的走向为减、增、减、增，但是中间增区间的长度不足1，

要想使函数在上单调递增，

只能，解得，矛盾，无解；

（iii），即，

此时，函数在上单调递增，

要想使函数在上单调递增，

所以需要，解得，所以，

综上，满足条件的的取值范围是.