题目内容
17.已知数列{an}的前n相和为Sn=$\frac{1}{2}$n(n+1),n∈N*,bn=3${\;}^{{a}_{n}}$+(-1)n-1an,则数列{bn}的前2n+1项和为$\frac{1}{2}•{3}^{2n+2}+n-\frac{1}{2}$.分析 由数列的前n项和求出数列{an}的通项公式,代入bn=3${\;}^{{a}_{n}}$+(-1)n-1an,然后利用数列的分组求和及等比数列的前n项和得答案.
解答 解:由Sn=$\frac{1}{2}$n(n+1),得${a}_{1}={S}_{1}=\frac{1}{2}×1×2=1$,
当n≥2时,an=Sn-Sn-1=$\frac{1}{2}n(n+1)-\frac{1}{2}(n-1)n$=n,
当n=1时上式成立,
∴an=n,
则bn=3${\;}^{{a}_{n}}$+(-1)n-1an=3n+(-1)n-1n,
∴数列{bn}的前2n+1项和为(31+32+…+32n+1)+[1-2+3-4+…+(2n-1)-2n+(2n+1)]
=$\frac{3(1-{3}^{2n+1})}{1-3}+n+1$=$\frac{1}{2}•{3}^{2n+2}+n-\frac{1}{2}$.
故答案为:$\frac{1}{2}•{3}^{2n+2}+n-\frac{1}{2}$.
点评 本题考查了等差关系的确定,考查了数列的分组求和及等比数列的前n项和,是中档题.

练习册系列答案
相关题目
7.某产品的广告费用x(单位:万元)的统计数据如下表:
根据上表可得线性回归方程$\widehat{y}$=9.4x+9.1,表中有一数据模糊不清,请推算该数据的值为39.
| 广告费用x(单位:万元) | 2 | 3 | 4 | 5 |
| 利润y(单位:万元) | 26 | ● | 49 | 54 |
5.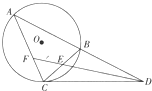 如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.
如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.
(Ⅰ)若∠ADC的平分线分别交BC、AC于点E、F,求证:CE=CF;
(Ⅱ)若CD=6,BC=5,求线段AC的长.
 如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.
如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.(Ⅰ)若∠ADC的平分线分别交BC、AC于点E、F,求证:CE=CF;
(Ⅱ)若CD=6,BC=5,求线段AC的长.
6.已知双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点为F,以原点为圆心,OF为半径的圆分别与双曲线Γ的一条渐近线及双曲线Γ交于M、N两点(其中M、N均为第一象限上的点),当MF∥ON时,双曲线Γ的离心离一定在区间( )
| A. | (1,$\frac{4}{3}$) | B. | ($\frac{4}{3}$,$\sqrt{2}$) | C. | ($\sqrt{2}$,$\sqrt{3}$) | D. | ($\sqrt{3}$,2) |