题目内容
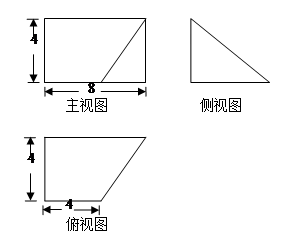
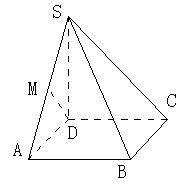
已知某几何体的直观图和三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形
(1)求证: ; (2)求证:
; (2)求证: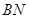
 ;
;
(3)设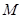 为
为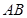 中点,在
中点,在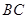 边上找一点
边上找一点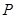 ,使
,使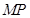
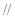 平面
平面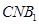 ,并求
,并求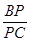 的值.
的值.
(1)根据三视图还原几何体,并能结合向量的知识建立空间直角坐标系,借助于法向量来得到证明。
(2)对于线面的垂直的证明,一般通过线线垂直的证明来得到线面垂直。
(3)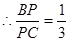
解析试题分析:解:(1)证明: 该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,
该几何体的正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,
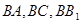 两两互相垂直。以
两两互相垂直。以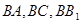 分别为
分别为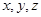 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则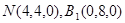 ,
,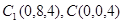 ,
,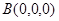 2分
2分
∵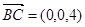 ,
, ,
, ,∴
,∴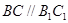
∵ ,
, ,
,
∴ 4分
4分
(2)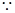
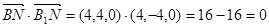 ,
,

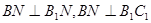 ,又
,又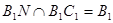

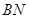
 8分
8分
(3)设 为
为 上一点,
上一点,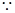
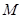 为
为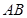 的中点,
的中点,
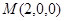 ,
, ,
,
设平面的一个法向量为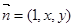 ,则有
,则有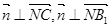 ,则有
,则有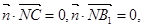
∴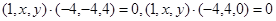 ,得
,得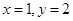 ,
,
∴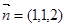 ,…10分
,…10分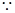
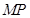 //平面
//平面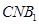 ,
,
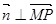 ,于是
,于是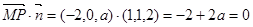
解得: 12分
12分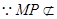 平面
平面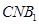 ,
,
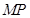 //平面
//平面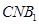 ,此时
,此时 ,
,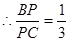 14分
14分
(注:此题用几何法参照酌情给分)
考点:空间中点线面的位置关系
点评:主要是考查了空间中的线面的平行和垂直的证明,熟练的掌握判定定理和性质定理是结题的关键,属于基础题。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
 为圆
为圆 的直径,点
的直径,点 、
、 在圆
在圆 所在的平面和圆
所在的平面和圆 ,
, .
.
 平面
平面 ;
; 的体积.
的体积. 中,
中, ,
, ,
, 为
为 中点.(Ⅰ)证明:
中点.(Ⅰ)证明: ;(Ⅱ)求
;(Ⅱ)求 与平面
与平面 所成角的正弦值;(Ⅲ)在棱
所成角的正弦值;(Ⅲ)在棱 上是否存在一点
上是否存在一点 ,使得
,使得
 ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
ABC=60。,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.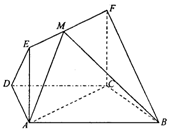
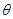 ,求
,求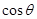 .
.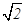 ,
,
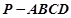 中,侧棱
中,侧棱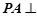 底面
底面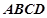 ,底面
,底面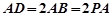 ,
,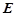 为
为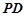 的上一点,且
的上一点,且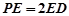 ,
,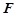 为PC的中点.
为PC的中点.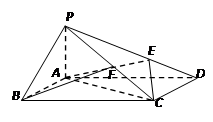

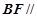 平面AEC;
平面AEC;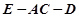 的余弦值.
的余弦值.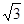 .
.
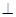 SC;
SC; 中,
中, 为正三角形,
为正三角形, ,
,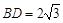 ,
, 与
与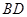 交于
交于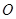 点.将
点.将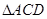 沿边
沿边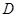 点至
点至 点,已知
点,已知 与平面
与平面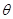 ,且
,且
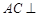 平面
平面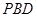 ;
;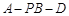 的余弦值为
的余弦值为 ,求
,求 的大小.
的大小. 