题目内容
(2012•葫芦岛模拟)已知椭圆
+
=1(a>b>0)的右焦点为F,离心率为
,过点F且倾斜角为60°的直线l与椭圆交于A、B两点(其中A点在x轴上方),则
的值等于( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| |AF| |
| |BF| |
分析:设椭圆的右准线为l,设A、B两点在l上的射影分别为C、D,连接AC、BD,过点A作AG⊥BD利用圆锥曲线的统一定义,再结合直角△ABG中,∠BAG=30°,可求出边之间的长度之比,可求
解答:解:如图,设椭圆的右准线为l,过A点作AC⊥l于C,过点B作BD⊥l于D,过A作AG⊥BD,垂直为D
在直角△ABG中,∠BAG=30°,
所以
AB=BG,…①
由圆锥曲线统一定义得:e=
=
=
∴|FB|=
|BD|,|AF|=
|AC|②
①②联立可得,BD-AC=2Bf-2AF=
(AF+BF)
∴AF=
BF
则
=
故选B
在直角△ABG中,∠BAG=30°,
所以
| 1 |
| 2 |
由圆锥曲线统一定义得:e=
| AF |
| AC |
| BF |
| BD |
| 1 |
| 2 |
∴|FB|=
| 1 |
| 2 |
| 1 |
| 2 |
①②联立可得,BD-AC=2Bf-2AF=
| 1 |
| 2 |
∴AF=
| 3 |
| 5 |
则
| |AF| |
| |BF| |
| 3 |
| 5 |
故选B
点评:本题考察了圆锥曲线的统一定义的应用,结合解含有60°的直角三角形,利用椭圆的离心率进行求解,属于几何方法,运算量小,方便快捷.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案
相关题目
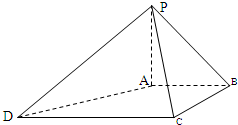 (2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=
(2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=