题目内容
(2012•葫芦岛模拟)袋中有6个小球,分别标有数字1,2,3,4,5,6,甲乙两人玩游戏,先由甲从袋中任意摸出一个小球,记下号码a后放回袋中,再由乙摸出一个小球,记下号码b,若|a-b|≤1,就称甲乙两人“有默契”,则甲乙两人“有默契”的概率为( )
分析:分别写出所有可能出现的结果,和所求事件所包含的基本事件,再根据古典概型的求法公式即可得解
解答:解:甲乙两个人摸球,所有可能的基本事件有:
(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6)
(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6)
(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3,6)
(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6)
(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6)
(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6,6)
共36种
事件“甲乙两人“有默契””所包含的基本事件有:(1,1)、(1,2)、(2,1)、(2,2)、(2,3)、(3,2)、(3,3)、(3,4)、(4,3)、(4,4)、(4,5)、(5,4)、(5,5)、(5,6)、(6,5)、(6,6)共16种
∴甲乙两人“有默契”的概率为P=
=
故选D
(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6)
(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6)
(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3,6)
(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6)
(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6)
(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6,6)
共36种
事件“甲乙两人“有默契””所包含的基本事件有:(1,1)、(1,2)、(2,1)、(2,2)、(2,3)、(3,2)、(3,3)、(3,4)、(4,3)、(4,4)、(4,5)、(5,4)、(5,5)、(5,6)、(6,5)、(6,6)共16种
∴甲乙两人“有默契”的概率为P=
| 16 |
| 36 |
| 4 |
| 9 |
故选D
点评:本题考查古典概型及其求法,概率=
,要求准确写出总的基本事件数和所求事件包含的基本事件数,要做到不重不漏.属简单题
| 所求事件所包含的基本事件数 |
| 总的基本事件数 |

练习册系列答案
相关题目
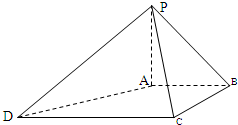 (2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=
(2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=