题目内容
中心为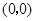 , 一个焦点为
, 一个焦点为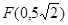 的椭圆,截直线
的椭圆,截直线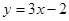 所得弦中点的横坐标为
所得弦中点的横坐标为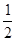 ,则该椭圆方程是( )
,则该椭圆方程是( )
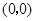 , 一个焦点为
, 一个焦点为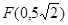 的椭圆,截直线
的椭圆,截直线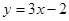 所得弦中点的横坐标为
所得弦中点的横坐标为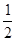 ,则该椭圆方程是( )
,则该椭圆方程是( )A.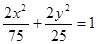 | B.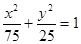 |
C.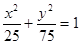 | D.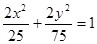 |
C
试题分析:
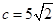 ,设椭圆方程为:
,设椭圆方程为: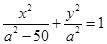 ,联立方程得
,联立方程得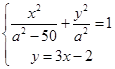 ,
,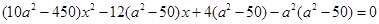 ,由韦达定理:
,由韦达定理: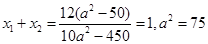 ,所以椭圆方程为
,所以椭圆方程为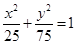 .
.
练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
题目内容
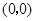 , 一个焦点为
, 一个焦点为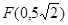 的椭圆,截直线
的椭圆,截直线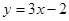 所得弦中点的横坐标为
所得弦中点的横坐标为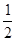 ,则该椭圆方程是( )
,则该椭圆方程是( )A.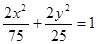 | B.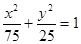 |
C.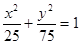 | D.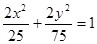 |
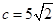 ,设椭圆方程为:
,设椭圆方程为: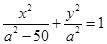 ,联立方程得
,联立方程得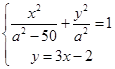 ,
,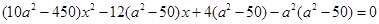 ,由韦达定理:
,由韦达定理: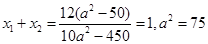 ,所以椭圆方程为
,所以椭圆方程为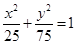 .
.
 计算高手系列答案
计算高手系列答案