题目内容
13.已知定点A(3,4),点P为抛物线y2=4x上一动点,点P到直线x=-3的距离为d,则|PA|+d的最小值是( )| A. | 2$\sqrt{5}$+2 | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$+2 | D. | 4$\sqrt{5}$ |
分析 先根据抛物线方程求出准线方程与焦点坐标,根据点A在抛物线外可得到|PA|+d的最小值为|AF|+2,再由两点间的距离公式可得答案.
解答 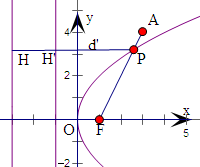 解:∵抛物线y2=4x的准线方程为x=-1,焦点F坐标(1,0),
解:∵抛物线y2=4x的准线方程为x=-1,焦点F坐标(1,0),
因为点A(3,4)在抛物线外,
设点P到直线x=-1的距离为d',
则d=d'+2,
根据抛物线的定义可得,
|PA|+d=|PA|+d'+2的最小值为|AF|+2=$\sqrt{(3-1)^{2}+(4-0)^{2}}$+2
=2$\sqrt{5}$+2,
故选A.
点评 本题考查抛物线的定义、方程和性质,主要考查定义法解题,运用两点间线段最短和两点的距离公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列说法正确的是( )
| A. | 圆锥的侧面展开图是一个等腰三角形 | |
| B. | 棱柱即是两个底面全等且其余各面都是矩形的多面体 | |
| C. | 任何一个棱台都可以补一个棱锥使它们组成一个新的棱锥 | |
| D. | 通过圆台侧面上一点,有无数条母线 |
1.已知g(x)是定义在R上的奇函数,且当x<0时,g(x)=-ln(1-x),函数f(x)=$\left\{\begin{array}{l}{{x}^{3},x≤0}\\{g(x),x>0}\end{array}\right.$,若f(2-x2)>f(x),则x的取值范围是( )
| A. | (-∞,-2)∪(1,+∞) | B. | (-∞,1)∪(2,+∞) | C. | (-2,1) | D. | (1,2) |
 的零点所在的区间为( )
的零点所在的区间为( ) B.
B.
 D.
D.
 的棱长为
的棱长为 ,半径为
,半径为 的圆
的圆 在平面
在平面 内,其圆心
内,其圆心 为圆
为圆 的外接球的表面积为( )
的外接球的表面积为( ) B.
B. C.
C.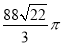 D.
D.