题目内容
2.用定积分的几何意义说明下列等式:(1)${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$cosθdθ=2${∫}_{0}^{\frac{π}{2}}$cosθdθ;
(2)${∫}_{π}^{π}$sinxdx=0.
分析 (1)根据余弦函数的对性得出${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$cosθdθ的几何意义是 余弦函数图象与直线x=$\frac{π}{2}$,x=$-\frac{π}{2}$,x轴,围成图形的面积,${∫}_{0}^{\frac{π}{2}}$cosθdθ的几何意义是 余弦函数图象与直线x=$\frac{π}{2}$,x=0,x轴,围成的图形的面积,可以得出积分的关系.
(2)根据正弦函数成中心对称,∫${\;}_{0}^{π}$sinxdx的几何意义是 正弦函数图象与直线x=π,x=0,x轴,围成的图形的面积,∫${\;}_{-π}^{0}$sinxdx的几何意义是 正弦函数图象与直线x=-π,x=0,x轴,围成的图形的面积的相反数,可以解释${∫}_{π}^{π}$sinxdx=0的几何意义.
解答 解:(1)${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$cosθdθ的几何意义是 余弦函数图象与直线x=$\frac{π}{2}$,x=$-\frac{π}{2}$,x轴,围成图形的面积,
${∫}_{0}^{\frac{π}{2}}$cosθdθ的几何意义是 余弦函数图象与直线x=$\frac{π}{2}$,x=0,x轴,围成的图形的面积,
根据函数的对称性得出,这两个面积成2倍关系,
∴${∫}_{-\frac{π}{2}}^{\frac{π}{2}}$cosθdθ=2${∫}_{0}^{\frac{π}{2}}$cosθdθ成立.
(2)${∫}_{π}^{π}$sinxdx=0.=0.
∵∫${\;}_{0}^{π}$sinxdx的几何意义是 正弦函数图象与直线x=π,x=0,x轴,围成的图形的面积,
∵∫${\;}_{-π}^{0}$sinxdx的几何意义是 正弦函数图象与直线x=-π,x=0,x轴,围成的图形的面积的相反数,
∴${∫}_{π}^{π}$sinxdx=∫${\;}_{-π}^{0}$sinxdx+∫${\;}_{0}^{π}$sinxdx=0
点评 本小题主要考查定积分、定积分的几何意义,三角函数的图象和性质,等基础知识,考查考查数形结合思想.属于基础题.

| A. | 2$\sqrt{5}$+2 | B. | 2$\sqrt{5}$ | C. | 4$\sqrt{2}$+2 | D. | 4$\sqrt{5}$ |
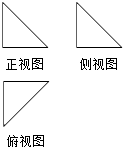
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
 与
与 都是I的子集(如图所示),则阴影部分所表示的集合为( )
都是I的子集(如图所示),则阴影部分所表示的集合为( )
 B.
B.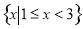
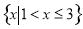 D.
D.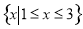
 如图,从圆O外一点P引圆的切线PC及割线PAB,C为切点.求证:AP•BC=AC•CP.
如图,从圆O外一点P引圆的切线PC及割线PAB,C为切点.求证:AP•BC=AC•CP.