题目内容

18．a是f（x）=2x-log$\frac{1}{2}$x的零点，若k＞a，则f（k）的值满足（　　）
A．f（k）=0B．f（k）＜0C．f（k）＞0D．f（k）的符号不确定

分析 先判断函数的单调性，进而根据a为零点，可得k＞a时，f（k）的符号．

解答 解：∵y=2x为增函数，y=log$\frac{1}{2}$x为减函数，
∴f（x）=2x-log$\frac{1}{2}$x为增函数；
若a是f（x）=2x-log$\frac{1}{2}$x的零点，则f（a）=0，
若k＞a，则f（k）＞0，
故选：C．

点评 本题考查的知识点是函数零点的判定定理，正确理解定义内容是解答的关键．

练习册系列答案
相关题目
8．在△ABC中，$|\overrightarrow{AB}|=2$，$|\overrightarrow{AC}|=3$，∠A=45°，M为BC边上的中点，分别求下列各式的值：
（1）$\overrightarrow{AB}$•$\overrightarrow{AC}$，
（2）$\overrightarrow{AB}$•$\overrightarrow{BC}$，
（3）$\overrightarrow{AB}$•$\overrightarrow{AM}$．
9．定义在R上的函数f（x）=$\frac{x}{{{x^2}+1}}$，若函数g（x）=f（x）+$\frac{mx}{1+x}$在区间（-1，1）上有且仅有两个不同的零点，求实数m的取值范围．
6．（1）求不等式的解集：|x-1|+|x+3|≥2．
（2）不等式|x-1|+|x+3|＞a，对一切实数x都成立，求实数a的取值范围．
13．y=x+$\frac{1}{x}$在点$（{2，\frac{5}{2}}）$处的切线的方程是3x-4y-4=0．
3．已知定义在R上的函数f（x）满足：①函数y=f（x-1）的图象关于（1，0）对称；②对于x∈R，$f（\frac{3}{4}-x）=f（\frac{3}{4}+x）$；③当$x∈（-\frac{3}{2}，-\frac{3}{4}]$时，f（x）=log2（-3x+1），则f（2012）=2．
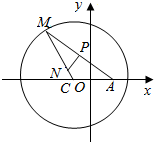10．如图所示，已知圆（x+3）2+y2=100，定点A（3，0），M为圆C上一动点，点P在AM上，点N在CM上，且满足$\overrightarrow{AM}$=2$\overrightarrow{AP}$，$\overrightarrow{NP}$•$\overrightarrow{AM}$=0，点N的轨迹为曲线E．
（1）求曲线E的方程；
（2）求过点Q（2，1）的弦的中点的轨迹方程．
7．已知关于x的不等式|x-3|+|x-5|≤m的解集不是空集，记m的最小值为t．
（Ⅰ）求t；
（Ⅱ）已知a＞0，b＞0，c=max{$\frac{1}{a}$，$\frac{{{a^2}+{b^2}}}{tb}$}，求证：c≥1．注：maxA表示数集A中的最大数．
8．已知函数y=${（\frac{1}{2}）}^{\sqrt{{-x}^{2}-3x+4}}$．
（1）求函数的定义域，值域；
（2）求函数的单调区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网