Question

(本小题满分10分)

已知函数f(x)= m·log₂x + t的图象经过点A（4，1）、点B（16，3）及点C（S_n，n），其中S_n为数列{a_n}的前n项和，n∈N^*.

（Ⅰ）求S_n和a_n；

（Ⅱ）设数列{b_n}的前n项和为T_n , b_n = f(a_n) – 1, 求不等式T_n£ b_n的解集，n∈N^*.

 

 

Answer 1

【答案】

（Ⅰ），

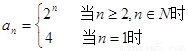
（Ⅱ）不等式的解集为{1, 2，3 }.

【解析】由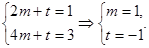                                                               

所以f(x)= log₂x  – 1 .由条件得: n = log₂S_n  – 1 .

得: ,                                                            

,

,

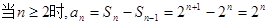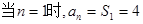所以 .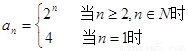                                                       

（2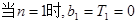）     , 不等式成立.                                                   

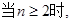  b_n = f(a_n) – 1= n  – 2 ,                                                       

 

,

解得: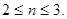    

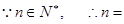2,3                                                                          

所求不等式的解集为{1, 2，3 }.