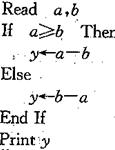题目内容
一种电脑屏幕保护画面,只有符号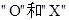 随机地反复出现,每秒钟变化一次,每次变化只出现
随机地反复出现,每秒钟变化一次,每次变化只出现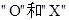 之一,其中出现
之一,其中出现 的概率为p,出现
的概率为p,出现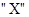 的概率为q,若第k次出现
的概率为q,若第k次出现 ,则记
,则记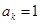 ;出现
;出现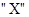 ,则记
,则记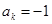 ,令
,令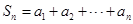 .
.
(1)当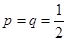 时,求
时,求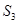 的分布列及数学期望.
的分布列及数学期望.
(2)当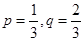 时,求
时,求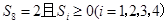 的概率.
的概率.
(1)详见解析;(2)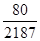 .
.
解析试题分析:(1)先分析 的取值,
的取值,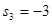 代表3次都是
代表3次都是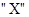 ,
,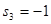 代表其中一次是
代表其中一次是 ,两次是
,两次是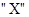 ,同理其他情况,
,同理其他情况,
(2)当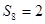 时,即前八秒出现“
时,即前八秒出现“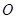 ”5次和“
”5次和“ ”3次,又已知
”3次,又已知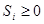 (i=1,2,3,4),可分前4次有2,3,或4次出现
(i=1,2,3,4),可分前4次有2,3,或4次出现 的情况,然后求出概率.
的情况,然后求出概率.
解:(1)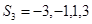
 ,
, 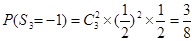
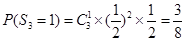
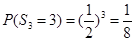
3 1 1 3 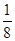
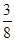
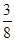
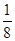
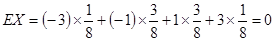
(2)前4次有2次出现 的概率是
的概率是 
前4次有3次出现 的概率是
的概率是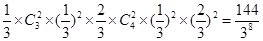
前4次有4次出现 的概率是
的概率是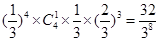
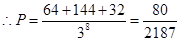
考点:1.相互独立事件的概率;2.分布列和期望

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
如图,A地到火车站共有两条路径 和
和 ,据统计,通过两条路径所用的时间互不影响,所用时间落在个时间段内的频率如下表:
,据统计,通过两条路径所用的时间互不影响,所用时间落在个时间段内的频率如下表: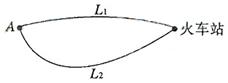
| 时间(分钟) | 10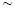 20 20 | 20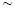 30 30 | 30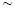 40 40 | 40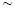 50 50 | 50 60 60 |
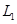 的频率 的频率 | 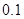 | 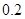 | 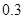 | 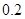 | 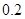 |
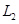 的频率 的频率 | 0 | 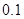 | 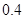 | 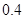 | 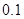 |
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站.
(1)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(2)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(1)的选择方案,求X的分布列和数学期望 .
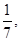 现不放回从袋中摸取球,每次摸一球,直到取到白球时即终止,每个球在每一次被取出的机会是等可能的,用
现不放回从袋中摸取球,每次摸一球,直到取到白球时即终止,每个球在每一次被取出的机会是等可能的,用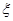 表示取球终止时所需要的取球次数.
表示取球终止时所需要的取球次数.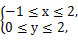 从区域W中随机取点M(x,y).
从区域W中随机取点M(x,y).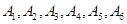 (如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为
(如图)这六个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为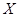 ,若
,若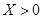 就去打球,若
就去打球,若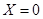 就去唱歌,若
就去唱歌,若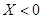 就去下棋。
就去下棋。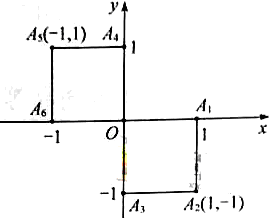
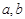 ,按以下程序进行运算:
,按以下程序进行运算: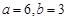 ,求程序运行后计算机输出的y的值;
,求程序运行后计算机输出的y的值;