题目内容
解答题：要求写出文字说明、证明过程和演算步骤
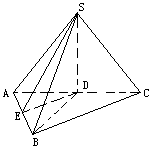
在三棱锥S－ABC中，侧面SAC⊥底面ABC，△SAC是边长为4的正三角形，△ACB为直角三角形，∠ACB＝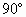
，BC＝4
．
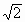(Ⅰ)求证：侧面SAC⊥侧面BSC；
(Ⅱ)求SB与底面ABC所成角；
(Ⅲ)求二面角S—AB—C的正切值．
答案：
解析：
解析：
|
(1)证明：∵∠ACB＝ 又面SAC⊥面ABC，面SAC∩面ABC＝AC ∴BC⊥面SAC 又BCÌ 面SBC ∴面SAC⊥面BSC (2)解：取AC的中点D，连SD、BD ∵△SAC为正三角形，边长为4 ∴SD⊥AC且SD＝2 又 面SAC⊥面ABC ∴SD⊥面ABC ∴∠SBD为SB与面ABC所成角 在Rt△BCD中，∠BCA＝Rt∠，BC＝4 ∴BD＝6 在Rt△SBD中，SD＝2 ∴∠SBD＝ (3)解：过D作DE⊥AB于E，连SE则SE⊥AB ∠SED为S－AB－C的平面角 在△ABC与△ADE中 AB＝4 ∴ ∴ ∴tan∠SED |
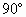，即BC⊥AC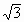
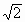，CD＝2
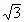，BD＝6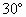
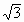，△ABC∽△ADE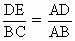
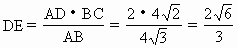
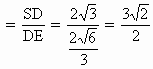
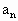练习册系列答案
相关题目
}是由正数组成的等比数列，数列{
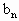}满足：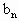
＝
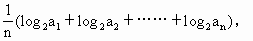
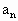}的公比为q，若数列{
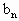}的前n项和存在最大值，求q的取值范围；
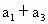＝20，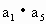
＝16，从数列{
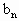}中依次取出第2项，第4项，第8项，……第
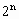项，……，组成数列{
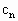}，求数列{
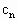}的前n项和．
＋
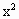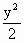＝1，点P(
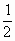，1)是椭圆内的定点，过点P的直线l与椭圆C交于A、B两点，点Q为线段AB的中点，求
＝(1，x)，
＝(x2＋x，－x)，m为实数，求使
成立的x的范围．