题目内容
已知向量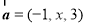 ,
,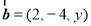 ,且
,且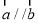 ,那么
,那么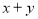 等于( )
等于( )
A.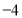 B.
B.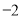 C.
C.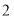 D.
D.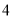
A
【解析】
试题分析:因为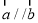 ,所以
,所以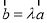 ,所以
,所以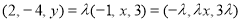 ,所以
,所以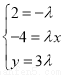 ,解得
,解得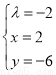 ,所以
,所以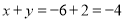 ,选答案A.
,选答案A.
考点:空间向量平行的坐标关系.

练习册系列答案
相关题目
题目内容
已知向量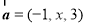 ,
,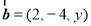 ,且
,且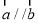 ,那么
,那么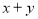 等于( )
等于( )
A.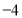 B.
B.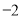 C.
C.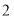 D.
D.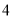
A
【解析】
试题分析:因为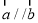 ,所以
,所以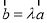 ,所以
,所以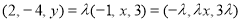 ,所以
,所以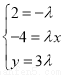 ,解得
,解得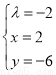 ,所以
,所以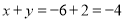 ,选答案A.
,选答案A.
考点:空间向量平行的坐标关系.
