题目内容
已知四棱锥![]() (如图)底面是边长为2的正方形.侧棱
(如图)底面是边长为2的正方形.侧棱![]() 底面
底面![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 于
于![]() 。
。
(Ⅰ)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求PA的长;
,求PA的长;
(Ⅲ)在条件(Ⅱ)下,求二面角![]() 的余弦值。
的余弦值。
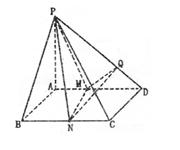
(1)证明见解析(2)2 (3)![]()
解析:
(Ⅰ)证明:∵PA⊥底面ABCD,MN![]() 底面ABCD
底面ABCD
∴MN⊥PA 又MN⊥AD 且PA∩AD=A
∴MN⊥平面PAD ………………3分
MN![]() 平面PMN ∴平面PMN⊥平面PAD …………4分
平面PMN ∴平面PMN⊥平面PAD …………4分
(Ⅱ)∵BC⊥BA BC⊥PA PA∩BA=A ∴BC⊥平面PBA
∴∠BPC为直线PC与平面PBA所成的角
即![]() …………7分
…………7分
在Rt△PBC中,PC=BC/sin∠BPC=![]()
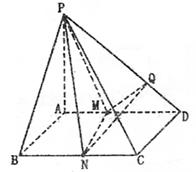
∴![]() ………………10分
………………10分
(Ⅲ)由(Ⅰ)MN⊥平面PAD知 PM⊥MN MQ⊥MN
∴∠PMQ即为二面角P—MN—Q的平面角 …………12分
而![]()
∴![]() …………14分
…………14分

练习册系列答案
相关题目
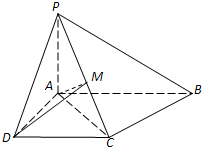 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.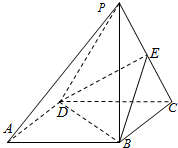 如图,已知四棱锥P-ABCD中,底面ABCD为正方形,侧面PDC为正三角形,且面PDC⊥面ABCD,E为PC中点.
如图,已知四棱锥P-ABCD中,底面ABCD为正方形,侧面PDC为正三角形,且面PDC⊥面ABCD,E为PC中点.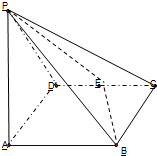 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成60°角.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠BCD=60°,BC=1,E为CD的中点,PC与平面ABCD成60°角.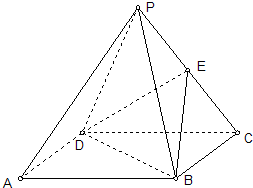 如图:已知四棱锥P-ABCD中,底面四边形为正方形,侧面PDC为正三角形,且平面PDC⊥底面ABCD,E为PC中点.
如图:已知四棱锥P-ABCD中,底面四边形为正方形,侧面PDC为正三角形,且平面PDC⊥底面ABCD,E为PC中点.