题目内容
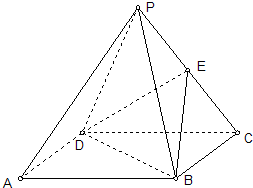如图：已知四棱锥P-ABCD中，底面四边形为正方形，侧面PDC为正三角形，且平面PDC⊥底面ABCD，E为PC中点．（1）求证：平面EDB⊥平面PBC；
（2）求二面角B-DE-C的平面角的正切值．
分析：（1）要证两个平面互相垂直，常规的想法是：证明其中一个平面过另一个平面的一条垂线，由于侧面PDC为正三角形，所以，DE⊥PC，那么我们自然想到：是否有DE⊥平面PBC，由此可证结论；
（2）确定∠BEC就是二面角B-DE-C的平面角，在Rt△ECB中，可求二面角B-DE-C的平面角的正切值．
（2）确定∠BEC就是二面角B-DE-C的平面角，在Rt△ECB中，可求二面角B-DE-C的平面角的正切值．
解答：（1）证明：∵面PDC⊥底面ABCD，交线为DC，∴DE在平面ABCD内的射影就是DC．
在正方形ABCD中，DC⊥CB，∴DE⊥CB．
又PC∩BC=C，PC，BC?面PBC，∴DE⊥面PBC．
又DE?面EDB，
∴平面EDB⊥平面PBC．
（2）解：由（1）的证明可知：DE⊥面PBC，所以，∠BEC就是二面角B-DE-C的平面角．
∵面PDC⊥底面ABCD，交线为DC，平面ABCD内的直线CB⊥DC．
∴CB⊥面PDC．
又PC?面PDC，∴CB⊥PC．
在Rt△ECB中，tan∠BEC=
=2．
在正方形ABCD中，DC⊥CB，∴DE⊥CB．
又PC∩BC=C，PC，BC?面PBC，∴DE⊥面PBC．
又DE?面EDB，
∴平面EDB⊥平面PBC．
（2）解：由（1）的证明可知：DE⊥面PBC，所以，∠BEC就是二面角B-DE-C的平面角．
∵面PDC⊥底面ABCD，交线为DC，平面ABCD内的直线CB⊥DC．
∴CB⊥面PDC．
又PC?面PDC，∴CB⊥PC．
在Rt△ECB中，tan∠BEC=
| BC |
| CE |
点评：本题考查面面垂直，考查线面垂直，考查面面角，解题的关键是掌握面面垂直的判定方法，正确作出面面角．
练习册系列答案
发散思维新课堂系列答案
相关题目
如图：已知四棱锥P-ABCD中，PD⊥平面ABCD，ABCD是正方形，E是PA的中点，
如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
如图，已知四棱锥P-ABCD的底面为菱形，∠BCD=60°，PD⊥AD．点E是BC边上的中点．
（2012•崇明县二模）如图，已知四棱锥P-ABCD的底面ABCD为正方形，PA⊥平面ABCD，E、F分别是BC，PC的中点，AB=2，AP=2．
（2012•吉林二模）如图，已知四棱锥P-ABCD的底面是正方形，PA⊥面ABCD，且PA=AD=2，点M，N分别在PD，PC上，