题目内容
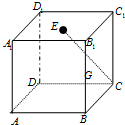
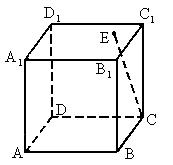
 如图,一块正方体形木料的上底面正方形ABCD中心为E,经过点E在上底面画直线与CE垂直,这样的直线可画( )
如图,一块正方体形木料的上底面正方形ABCD中心为E,经过点E在上底面画直线与CE垂直,这样的直线可画( )分析:设经过点E在上底面画直线与CE垂直的直线为l,根据正方体的性质,得到CC1⊥平面A1B1C1D1,从而有CC1⊥l.进一步得到l⊥平面CC1E,可得l⊥C1E,而在平面A1B1C1D1中,经过点E与C1E垂直的直线有且只有一条,因此可得正确答案.
解答: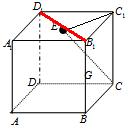 解:设经过点E在上底面画直线与CE垂直的直线为l,
解:设经过点E在上底面画直线与CE垂直的直线为l,
∵ABCD-A1B1C1D1是正方体
∴CC1⊥平面A1B1C1D1
∵l?平面A1B1C1D1,
∴CC1⊥l,又CE⊥l,
∵CC1、CE是平面CC1E内的相交直线
∴l⊥平面CC1E
∵C1E?平面CC1E
∴l⊥C1E,
而在平面A1B1C1D1中,经过点E与C1E垂直的直线有且只有一条,
故选B.
 解:设经过点E在上底面画直线与CE垂直的直线为l,
解:设经过点E在上底面画直线与CE垂直的直线为l,∵ABCD-A1B1C1D1是正方体
∴CC1⊥平面A1B1C1D1
∵l?平面A1B1C1D1,
∴CC1⊥l,又CE⊥l,
∵CC1、CE是平面CC1E内的相交直线
∴l⊥平面CC1E
∵C1E?平面CC1E
∴l⊥C1E,
而在平面A1B1C1D1中,经过点E与C1E垂直的直线有且只有一条,
故选B.
点评:本题给出正方体内的一条直线,让我们寻找与之垂直的直线,着重考查了空间中直线与直线之间的位置关系、线面垂直的判定与性质等知识点,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
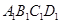 中心为
中心为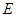 ,
, 垂直,这样的直线可画
垂直,这样的直线可画 条 B.
条 B.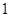 条
条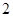 条
D.无数条
条
D.无数条