Question

(1)①证明：两角和的余弦公式C_(α＋β)：cos(α＋β)＝cos αcos β－sin αsin β；

②由C_(α＋β)推导两角和的正弦公式S_(α＋β)：sin(α＋β)＝sin αcos β＋cos αsin β.

(2)已知cos α＝－，α∈(π，π)，tan β＝－，β∈(，π)，求cos(α＋β)．

Answer 1

解：(1)证明：①如图，在直角坐标系xOy内作单位圆O，并作出角α，β与－β， 使角α的始边为Ox，交⊙O于点P₁，终边交⊙O于点P₂；角β的始边为OP₂，终边交⊙O于点P₃；角－β的始边为Ox，终边交⊙O于点P₄，则P₁(1，0)，P₂(cos α，sin α)，P₃(cos(α＋β)，sin(α＋β))，P₄(cos(－β)，sin(－β))．

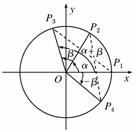
由P₁P₃＝P₂P₄及两点间的距离公式，得

[cos(α＋β)－1]²＋sin²(α＋β)

＝[cos(－β)－cos α]²

＋[sin(－β)－sin α]²，

展开并整理，得2－2cos (α＋β)＝2－2(cos αcos β－sin αsin β)．

∴cos(α＋β)

＝cos αcos β－sin αsin β.

②由①易得，cos(－α)＝sin α，sin(－α)＝cos α.

sin(α＋β)＝cos[－(α＋β)]＝cos[(－α)＋(－β)]

＝cos(－α)cos(－β)－sin(－α)sin(－β)

＝sin αcos β＋cos αsin β.

∴sin(α＋β)＝sin αcos β＋cos αsin β.

(2)∵α∈(π，π)，cos α＝－.

∴sin α＝－.∵β∈(，π)，tan β＝－.

∴cos β＝－，sin β＝.

cos(α＋β)＝cos αcos β－sin αsin β

＝(－)×(－)－(－)×＝.