题目内容

已知平面α∥平面β，P是α、β外一点，过P点的两条直线PAC、PBD分别交α于A、B，交β于C、D，且PA=6，AC=9，AB=8，则CD的长为
 
．
分析：有面面平行，可得线线平行，AB∥CD，在利用相似三角形的相似比可得CD的长
解答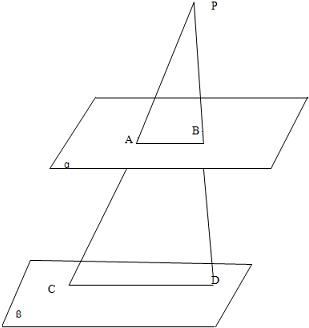：精英家教网解：如图所示，因为平面α∥平面β，
所以AB∥CD，
∴△PAB～△PCD，
∴
PA
PC
=
AB
CD

∴CD=
8×15
6
=20．
当P在平面α与平面β之间时，
∴
PA
PC
=
AB
CD

∴CD=
8×3
6
=4．
故答案为：20或4．
点评：面面平行的性质定理的应用问题，往往涉及面面平行的判定，线面平行的判定与性质的综合应用．解题时，要注意三种平行关系之间的相互转化．
练习册系列答案
相关题目
16、如图：已知平面α∥平面β，点A、B在平面α内，点C、D在β内，直线AB与CD是异面直线，点E、F、G、H分别是线段AC、BC、BD、AD的中点，求证：
（Ⅰ）E、F、G、H四点共面；
（Ⅱ）平面EFGH∥平面β．
设V是已知平面M上所有向量的集合，对于映射f：V→V，a∈V，记a的象为f（a）．若映射f：V→V满足：对所有a、b∈V及任意实数λ，μ都有f（λa+μb）=λf（a）+μf（b），则f称为平面M上的线性变换．下列命题中假命题是（　　）
给出下列四个命题
①过平面外一定点有且只有一个平面与已知平面垂直；
②过空间一定点有且只有一条直线与已知平面垂直；
③过平面外一定直线有且只有一个平面与已知平面垂直；
④垂直于同一平面的两个平面可能互相平行，也可能相交；
⑤垂直于同一条直线的两个平面平行；
⑥平行于同一个平面的两直线不是平行就是相交．
其中正确命题的序号为
②④⑤
②④⑤
．

已知下列四个命题，其中真命题的序号是（    ）

① 若一条直线垂直于一个平面内无数条直线，则这条直线与这个平面垂直；

② 若一条直线平行于一个平面，则垂直于这条直线的直线必垂直于这个平面；

③ 若一条直线平行一个平面，另一条直线垂直这个平面，则这两条直线垂直；

④ 若两条直线垂直，则过其中一条直线有唯一一个平面与另外一条直线垂直；

A.①②        B.②③         C.②④         D.③④

 

如图：已知平面//平面,点A、B在平面内，点C、D在内，直线AB与CD是异面直线，点E、F、G、H分别是线段AC、BC、BD、AD的中点，

求证：（Ⅰ）E、F、G、H四点共面；

（Ⅱ）平面EFGH//平面.

 

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网