题目内容
如图:已知平面 //平面
//平面 ,点A、B在平面
,点A、B在平面 内,点C、D在
内,点C、D在 内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
内,直线AB与CD是异面直线,点E、F、G、H分别是线段AC、BC、BD、AD的中点,
求证:(Ⅰ)E、F、G、H四点共面;
(Ⅱ)平面EFGH//平面 .
.

【答案】
(Ⅰ)∵点E、F是线段AC、BC的中点,∴EF∥AB,
又∵G、H是线段BD、AD的中点,∴GH∥AB,
∴EF∥GH, 因此: E、F、G、H四点共面;
(Ⅱ)∵平面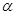 //平面
//平面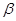 ,点A、B在平面
,点A、B在平面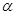 内,∴AB//平面
内,∴AB//平面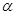
设平面ABC与平面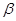 的交线为CP,
的交线为CP,
∵直线AB与CD是异面直线, ∴CP与CD是交线,
∵AB//平面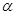 , ∴AB//CP, 又EF∥AB, ∴EF//CP,∴EF∥平面
, ∴AB//CP, 又EF∥AB, ∴EF//CP,∴EF∥平面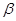 ,
,
∵点E、H是线段AC、AD的中点,∴EH∥CD, ∴EH∥平面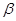 ,
,
因此:平面EFGH//平面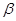
【解析】略

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 9、如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
9、如图,已知四边形ABCD是平行四边形,点P是平面ABCD外的一点,则在四棱锥P-ABCD中,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
 如图,已知直角梯ACDE所在的平面垂直于平ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
如图,已知直角梯ACDE所在的平面垂直于平ABC,∠BAC=∠ACD=90°,∠EAC=60°,AB=AC=AE.
