题目内容
已知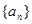 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn,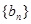 是等比数列,且
是等比数列,且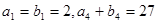 ,
,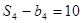 .
.
(Ⅰ)求数列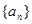 与
与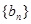 的通项公式;
的通项公式;
(Ⅱ)记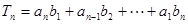 ,
,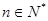 ,证明
,证明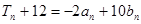 (
(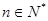 ).
).
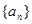 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn,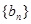 是等比数列,且
是等比数列,且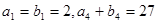 ,
,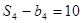 .
.(Ⅰ)求数列
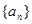 与
与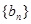 的通项公式;
的通项公式;(Ⅱ)记
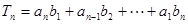 ,
,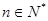 ,证明
,证明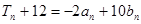 (
(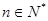 ).
).(1)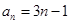 ,
, ,
,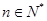 (2)
(2)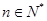 ,
,
【考点定位】本小题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和等基础知识.考查化归与转化的思想方法.考查运算能力、推理论证能力.该试题命制比较直接,没有什么隐含的条件,就是等比与等差数列的综合应用,但方法多样,第二问可以用错位相减法求解证明,也可用数学归纳法证明,给学生思维空间留有余地,符合高考命题选拔性的原则
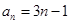 ,
, ,
,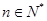 (2)
(2)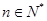 ,
,
【考点定位】本小题主要考查等差数列与等比数列的概念、通项公式、前n项和公式、数列求和等基础知识.考查化归与转化的思想方法.考查运算能力、推理论证能力.该试题命制比较直接,没有什么隐含的条件,就是等比与等差数列的综合应用,但方法多样,第二问可以用错位相减法求解证明,也可用数学归纳法证明,给学生思维空间留有余地,符合高考命题选拔性的原则
(1)设等差数列 的公差为d,等比数列
的公差为d,等比数列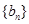 的公比为q.
的公比为q.
由 ,得
,得 ,
, ,
, .
.
由条件,得方程组 ,解得
,解得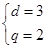
所以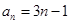 ,
, ,
,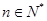 .
.
(2)证明:(方法一)
由(1)得
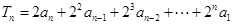 ①
①
 ②
②
由②-①得


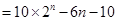
而
故 ,
,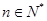
(方法二:数学归纳法)
① 当n=1时, ,
, ,故等式成立.
,故等式成立.
② 假设当n=k时等式成立,即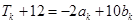 ,则当n=k+1时,有:
,则当n=k+1时,有:


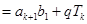
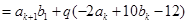


即 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立
由①和②,可知对任意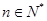 ,
, 成立.
成立.
 的公差为d,等比数列
的公差为d,等比数列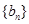 的公比为q.
的公比为q.由
 ,得
,得 ,
, ,
, .
.由条件,得方程组
 ,解得
,解得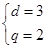
所以
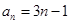 ,
, ,
,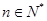 .
.(2)证明:(方法一)
由(1)得
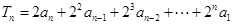 ①
① ②
②由②-①得


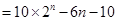
而

故
 ,
,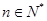
(方法二:数学归纳法)
① 当n=1时,
 ,
, ,故等式成立.
,故等式成立.② 假设当n=k时等式成立,即
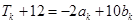 ,则当n=k+1时,有:
,则当n=k+1时,有:

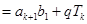
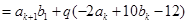


即
 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立由①和②,可知对任意
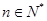 ,
, 成立.
成立.
练习册系列答案
相关题目
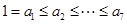 ,其中
,其中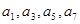 成公比为q的等比数列,
成公比为q的等比数列,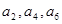 成公差为1的等差数列,则q的最小值是( )
成公差为1的等差数列,则q的最小值是( )



 是等比数列,首项
是等比数列,首项
 是等差数列,且
是等差数列,且 ,求数列
,求数列 项的和
项的和 是等差数列,其前n项和为
是等差数列,其前n项和为 ,
,  是等比数列,且
是等比数列,且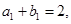


 求证:
求证: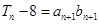 ,
, 。
。 中,
中, 是前
是前 项和,若
项和,若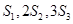 成等差数列,则数列
成等差数列,则数列
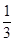


 中,已知
中,已知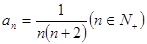 ,则
,则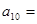 ▲ .
▲ .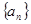 中,已知
中,已知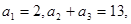 则
则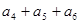 等于
等于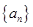 的前
的前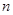 项和为
项和为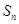 ,若
,若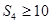 ,
,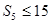 ,则
,则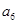 的最大值为 .
的最大值为 .