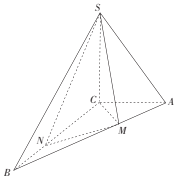
题目内容
【题目】如图,△ABC的内切圆分别与边BC、CA、AB切于点D、E、F,AD与BE交于点P,设点P关于直线EF、FD、DE的对称点分别X、Y、Z.证明:AX、BY、CZ三线共点.
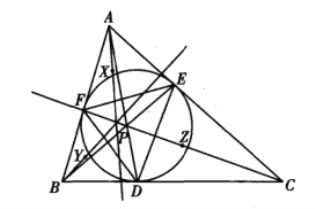
【答案】见解析
【解析】
设直线AX与EF的交点为M,直线BY与FD的交点为N,直线CZ与DE的交点为L,直线PA与EF的交点为R,直线PB与FD的交点为S,直线PC与DE的交点为T.
由直线束EA、EF、EB、ED为调和线束,知A、R、P、D成调和点列,且EF为∠AXP的平分线.故DM⊥EF.
类似地,EN⊥FD,FL⊥DE.
因此,DM、EN、FL三线共点于△DEF的垂心.
于是,![]() .
.
又由正弦定理知![]() .
.
类似地,![]() .
.
则![]() .
.
由角元塞瓦定理的逆定理得AX、BY、CZ三线共点.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某服装公司,为确定明年![]() 类服装的广告费用,对往年广告费
类服装的广告费用,对往年广告费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:件)和年利润
(单位:件)和年利润![]() (单位:千元)的影响.对2011-2018广告费
(单位:千元)的影响.对2011-2018广告费![]() 和年销售量
和年销售量![]() 数据进行了处理,分析出以下散点图和统计量:
数据进行了处理,分析出以下散点图和统计量:

|
|
|
|
|
|
|
45 | 580 | 2025 | 297 | 1600 | 960 | 1440 |
表中![]()
(1)由散点图可知,![]() 和
和![]() 更适合作为年销售量
更适合作为年销售量![]() 关于年广告费
关于年广告费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果和表中数据求![]() 关于
关于![]() 的回归方程.
的回归方程.
(3)已知该类服装年利率![]() 与
与![]() 的关系为
的关系为![]() .由(2)回答以下问题:年广告费用
.由(2)回答以下问题:年广告费用![]() 等于60时,年销售量及年利润的预报值为多少?年广告费用为何值时,年利率的预报值最小?
等于60时,年销售量及年利润的预报值为多少?年广告费用为何值时,年利率的预报值最小?
对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
【题目】某面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,以便利润最大化,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,以便利润最大化,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该店这款新面包每日出炉数设定为![]() 个
个
(i)求日需求量为![]() 个时的当日利润;
个时的当日利润;
(ii)求这![]() 天的日均利润.
天的日均利润.
相关公式: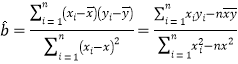 ,
,![]()