题目内容
已知抛物线y2=4x上一点M到焦点的距离为3,则点M到y轴的距离为 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先设出该点的坐标,根据抛物线的定义可知该点到准线的距离与其到焦点的距离相等,进而利用点到直线的距离求得x的值,
代入抛物线方程求得y值,即可得到所求点的坐标.
代入抛物线方程求得y值,即可得到所求点的坐标.
解答:
解:∵抛物线方程为y2=4x
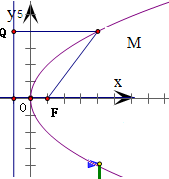
∴焦点为F(1,0),准线为l:x=-1
设所求点坐标为M(x,y)
作MQ⊥l于Q
根据抛物线定义可知M到准线的距离等于M、Q的距离
即x+1=3,解之得x=2,
代入抛物线方程求得y=±4
故点M坐标为:(2,y)
即点M到y轴的距离为2
故答案为:2.

∴焦点为F(1,0),准线为l:x=-1
设所求点坐标为M(x,y)
作MQ⊥l于Q
根据抛物线定义可知M到准线的距离等于M、Q的距离
即x+1=3,解之得x=2,
代入抛物线方程求得y=±4
故点M坐标为:(2,y)
即点M到y轴的距离为2
故答案为:2.
点评:本题主要考查了抛物线的简单性质.在涉及焦点弦和关于焦点的问题时常用抛物线的定义来解决.

练习册系列答案
相关题目
设等比数列{an}的公比为q,前n项和为Sn,若S8,S7,S9成等差数列,则公比q为( )
| A、q=1 |
| B、q=-2或q=1 |
| C、q=-2 |
| D、q=2或q=-1 |
三角形ABC中AB=2,AC=3,D为BC的中点,则
•
=( )
| AD |
| BC |
A、
| ||
B、-
| ||
| C、5 | ||
| D、-5 |
从1,2,3,4,5中任取两个不同的数字,构成一个两位数,则这个数字大于40的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|