题目内容
我们将具有下列性质的所有函数组成集合M：函数
，对任意
均满足
，当且仅当
时等号成立。
（1）若定义在(0，＋∞)上的函数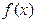
∈M，试比较
与
大小.
（2）设函数g(x)＝－x2，求证：g(x)∈M.
，对任意均满足，当且仅当时等号成立。（1）若定义在(0，＋∞)上的函数
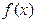∈M，试比较与大小.（2）设函数g(x)＝－x2，求证：g(x)∈M.
（1）<（2）证明略
<（2）证明略(1)对于，令
得<
(2)
,所以g(x)∈M
，令得<(2)
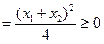
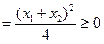
,所以g(x)∈M
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，是否存在不小于2的正整数
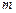，使得对于任意的正整数
都能被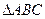
的三个内角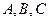
成等差数列，求证：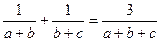
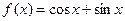,问是否存在
,
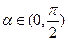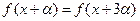恒成立？证明你的结论.
，
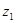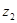对应的向量分别是
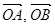，则复数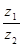
对应的点位于第 象限．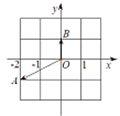
，求证：
的前n项和为
，令
，称
为数列
，
，……，
的“理想数”，已知数列
的“理想数”为2004，那么数列2，