题目内容
若直线mx+y-2m=0与直线(3m-4)x+y+1=0垂直,则m的值是( )A.-1或

B.1或

C.
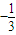 或-1
或-1D.
 或1
或1
【答案】分析:当直线的斜率不存在时,求出m的值,检验是否满足直线l1和直线l2垂直,当两直线的斜率都存在时,由斜率之积等于-1可得关于m的方程,解得m的值.
解答:解:当m=0时,直线l1:y=0,斜率等于0,l2:-4x+y+1=0,不满足直线l1和直线l2垂直.
当两直线的斜率都存在时,由斜率之积等于-1可得-m•(4-3m)=-1,解得m=1或 ,
,
综上得,m的值是 1 或 .
.
故选:B.
点评:本题主要考查两直线垂直的性质,两直线垂直斜率之积等于-1,注意考虑斜率不存在的情况,属于基础题.
解答:解:当m=0时,直线l1:y=0,斜率等于0,l2:-4x+y+1=0,不满足直线l1和直线l2垂直.
当两直线的斜率都存在时,由斜率之积等于-1可得-m•(4-3m)=-1,解得m=1或
 ,
,综上得,m的值是 1 或
 .
.故选:B.
点评:本题主要考查两直线垂直的性质,两直线垂直斜率之积等于-1,注意考虑斜率不存在的情况,属于基础题.

练习册系列答案
相关题目

 或-1
或-1

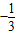 或-1
或-1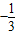 或1
或1