题目内容
已知函数f (x)=2sin2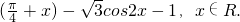
(1)若函数h (x)=f (x+t)的图象关于点 对称,且t∈(0,π),求t的值;
对称,且t∈(0,π),求t的值;
(2)设p:x∈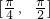 ,q:|f (x)-m|≤3,若p是q的充分不必要条件,求实数m的取值范围.
,q:|f (x)-m|≤3,若p是q的充分不必要条件,求实数m的取值范围.
解:(1)由题意知,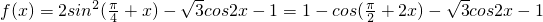
= ,
,
∴h(x)=f(x+t)=2sin( ),
),
∴h(x)的图象的对称中心为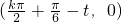 ,k∈Z,
,k∈Z,
又∵已知点 为h(x)的图象的一个对称中心,
为h(x)的图象的一个对称中心,
∴ ,
,
∵t∈(0,π),∴t=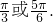
(2)若p成立,即当x∈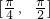 时,
时,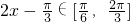 ,
,
∴ ,即f(x)∈[1,2],
,即f(x)∈[1,2],
由|f(x)-m|≤3得,m-3≤f(x)≤m+3,
∵p是q的充分不必要条件,∴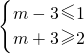 ,解得-1≤m≤4,
,解得-1≤m≤4,
即m的取值范围是[-1,4].
分析:(1)利用倍角公式和两角和差的正弦(余弦)公式,对函数f (x)的解析式进行变形后,求出函数h (x)的解析式,再根据正弦函数的对称性和t的范围求出t的值;
(2)根据x的范围求出“ ”的范围,由正弦函数的性质求出f (x)的值域,即p的范围;再求出绝对值不等式:|f (x)-m|≤3的解集,根据题意列出关于m的不等式,求出m的范围.
”的范围,由正弦函数的性质求出f (x)的值域,即p的范围;再求出绝对值不等式:|f (x)-m|≤3的解集,根据题意列出关于m的不等式,求出m的范围.
点评:本题考查了复合三角函数的性质问题,利用倍角公式和两角和差的正弦(余弦)公式对解析式进行化简,再根据正弦函数的性质进行求解,主要考查了“整体思想”和计算能力.
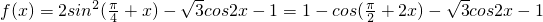
=
 ,
,∴h(x)=f(x+t)=2sin(
 ),
),∴h(x)的图象的对称中心为
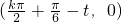 ,k∈Z,
,k∈Z,又∵已知点
 为h(x)的图象的一个对称中心,
为h(x)的图象的一个对称中心,∴
 ,
,∵t∈(0,π),∴t=
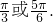
(2)若p成立,即当x∈
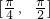 时,
时,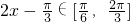 ,
,∴
 ,即f(x)∈[1,2],
,即f(x)∈[1,2],由|f(x)-m|≤3得,m-3≤f(x)≤m+3,
∵p是q的充分不必要条件,∴
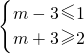 ,解得-1≤m≤4,
,解得-1≤m≤4,即m的取值范围是[-1,4].
分析:(1)利用倍角公式和两角和差的正弦(余弦)公式,对函数f (x)的解析式进行变形后,求出函数h (x)的解析式,再根据正弦函数的对称性和t的范围求出t的值;
(2)根据x的范围求出“
 ”的范围,由正弦函数的性质求出f (x)的值域,即p的范围;再求出绝对值不等式:|f (x)-m|≤3的解集,根据题意列出关于m的不等式,求出m的范围.
”的范围,由正弦函数的性质求出f (x)的值域,即p的范围;再求出绝对值不等式:|f (x)-m|≤3的解集,根据题意列出关于m的不等式,求出m的范围.点评:本题考查了复合三角函数的性质问题,利用倍角公式和两角和差的正弦(余弦)公式对解析式进行化简,再根据正弦函数的性质进行求解,主要考查了“整体思想”和计算能力.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|