题目内容
函数
，在区间（-π，π）上单调递增，则实数φ的取值范围为 ．
【答案】分析：求出函数的单调增区间，通过子集关系，确定实数φ的取值范围．
解答：解：函数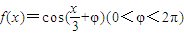
，由2kπ-π
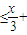φ≤2kπ，可得6kπ-3π-3φ≤x≤6kπ-3φ，由题意在区间（-π，π）上单调递增，
所以6kπ-3π-3φ≤-π 且 π≤6kπ-3φ，因为0＜φ＜2π，所以k=1，实数φ的取值范围为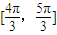
；
故答案为：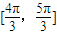
点评：本题是基础题，考查三角函数的单调性的应用，子集关系的理解，考查计算能力．
解答：解：函数
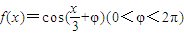，由2kπ-π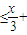φ≤2kπ，可得6kπ-3π-3φ≤x≤6kπ-3φ，由题意在区间（-π，π）上单调递增，所以6kπ-3π-3φ≤-π 且 π≤6kπ-3φ，因为0＜φ＜2π，所以k=1，实数φ的取值范围为
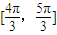；故答案为：
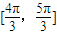
点评：本题是基础题，考查三角函数的单调性的应用，子集关系的理解，考查计算能力．
练习册系列答案
相关题目