题目内容
关于函数y=-x2+2|x|+3的单调性,下列叙述是否正确:“函数y=-x2+2|x|+3在x∈(-∞,-1]∪[0,1]上是增函数,在x∈[-1,0]∪[1,+∞)上为减函数.解:y=-x2+2|x|+3
=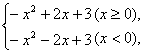 =
=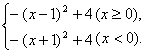
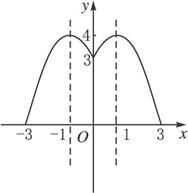
由函数的图象可看出,在(-∞,-1],[0,1]上函数是增函数,在[-1,0],[1,+∞)上函数是减函数,所以在(-∞,-1]∪[0,1]和[-1,0]∪[1,+∞)上不具有单调性.

练习册系列答案
相关题目
题目内容
关于函数y=-x2+2|x|+3的单调性,下列叙述是否正确:“函数y=-x2+2|x|+3在x∈(-∞,-1]∪[0,1]上是增函数,在x∈[-1,0]∪[1,+∞)上为减函数.解:y=-x2+2|x|+3
=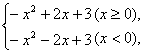 =
=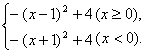

由函数的图象可看出,在(-∞,-1],[0,1]上函数是增函数,在[-1,0],[1,+∞)上函数是减函数,所以在(-∞,-1]∪[0,1]和[-1,0]∪[1,+∞)上不具有单调性.
