题目内容
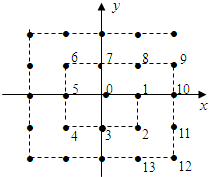 13、如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则表上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,则标签20092的格点的坐标为
13、如图,将平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则表上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,以此类推,则标签20092的格点的坐标为(1004,1005)
.分析:根据已知中平面直角坐标系的格点(横、纵坐标均为整数的点)按如下规则表上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)标5,点(-1,1)处标6,点(0,1)处标7,我们归纳出其中奇数平方坐标的位置出现的规律,即可得到答案.
解答:解:观察已知中点(1,0)处标1,即12,
点(2,1)处标9,即32,
点(3,2)处标25,即52,
…
由此推断
点(n+1,n)处标(2n+1)2,
当2n+1=2009时,n=1004
故标签20092的格点的坐标为(1005,1004)
故答案为:(1005,1004)
点(2,1)处标9,即32,
点(3,2)处标25,即52,
…
由此推断
点(n+1,n)处标(2n+1)2,
当2n+1=2009时,n=1004
故标签20092的格点的坐标为(1005,1004)
故答案为:(1005,1004)
点评:本题考查的知识点是归纳推理,其中根据已知平面直角坐标系的格点(横、纵坐标均为整数的点)的规则,找出表上数字标签所示的规律,是解答的关键.

练习册系列答案
相关题目
 (2012•泉州模拟)将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知
(2012•泉州模拟)将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知 将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知
将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知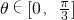 .
. 的坐标(要求将结果化简为形如(cosα,sinα)的形式);
的坐标(要求将结果化简为形如(cosα,sinα)的形式);

 (t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为 已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,
已知三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,