题目内容

已知函数f(x)＝ (sin2x－cos2x)－2sinxcosx.
(1)求f(x)的最小正周期；
(2)设x∈[－，]，求f(x)的值域和单调递增区间．

(1) 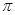 (2),

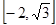解析试题分析：
在解决所有问题之前,得先将函数式化简为形式.而化简三角函数式需要注意三方面:角,名,次数.首先将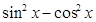利用余弦二倍角公式化简,然后将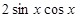利用正弦二倍角公式化简,此时函数式中的角都是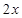,最后利用辅助角公式化名即可.
(1)根据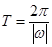求得最小正周期.
(2)根据角的范围,确定函数的值域,利用单调性确定单调增区间.
试题解析：化简
(1)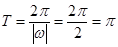,所以最小正周期为.
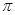(2)因为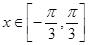,所以.
则根据正弦函数的图像可知,
所以函数的值域为.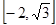
根据函数式可知,当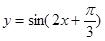递减时,递增.
则令,解得.
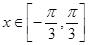又因为,所以.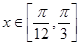
故的单调递增区间为 .
考点：三角函数式的化简;三角函数最小正周期;三角函数单调性.

练习册系列答案
相关题目

保持正弦曲线上所有点的纵坐标不变，横坐标缩短为原来的，再将图像沿 轴向右平移 个单位，得到函数 的图像.
（1）写出的表达式，并计算.
（2）求出在 上的值域.

如图，某市新体育公园的中心广场平面图如图所示，在y轴左侧的观光道曲线段是函数，时的图象且最高点B（-1，4），在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A，和的值；⑵现要在右侧的半圆中修建一条步行道CDO（单位：米），在点C与半圆弧上的一点D之间设计为直线段（造价为2万元/米），从D到点O之间设计为沿半圆弧的弧形（造价为1万元/米）．设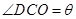(弧度)，试用来表示修建步行道的造价预算，并求造价预算的最大值？（注：只考虑步行道的长度，不考虑步行道的宽度）

设函数的最小正周期为
（1）求的值；
（2）若函数的图像是由的图像向右平移个单位长度得到，求的单调增区间．

设函数.
（1）求的最小正周期；
（2）若函数的图像向右、向上分别平移个单位长度得到的图像，求在的最大值.

某实验室一天的温度（单位：）随时间（单位：）的变化近似满足函数关系；
.
（1）求实验室这一天上午8时的温度；
（2）求实验室这一天的最大温差.

（本小题满分12分）
已知函数.
（1）求的值；
（2）求函数的最小正周期及单调递增区间.

已知sin α<0，tan α>0.
(1)求α角的集合；
(2)求终边所在的象限；
(3)试判断tansincos的符号．

已知sin θ、cos θ是关于x的方程x2－ax＋a＝0(a∈R)的两个根．
(1)求cos＋sin的值；
(2)求tan(π－θ)－的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网