题目内容
数列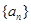 的通项公式
的通项公式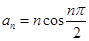 ,其前
,其前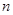 项和为
项和为 ,则
,则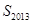 等于( )
等于( )
| A.1006 | B.2012 | C.503 | D.0 |
A
解析试题分析:由于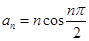 ,a1+a2+a3+a4=a5+a6+a7+a8=…=2,则四项结合的和为定值,可求又∵f(n)=
,a1+a2+a3+a4=a5+a6+a7+a8=…=2,则四项结合的和为定值,可求又∵f(n)=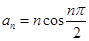 是以T=4为周期的周期函数,∴a1+a2+a3+a4=(0-2+0+4)=2,a5+a6+a7+a8=(0-6+0+8)=2,,…,a2009+a2010+a2011+a2012=(0-2010+0+2012)=2, S2012=a1+a2+a3+a4+…+a2012+ a2013,=(0-2+0+4)+(0-6+0+8)+…+(0-2010+0+2012)+0,=2×503=1006,故选A
是以T=4为周期的周期函数,∴a1+a2+a3+a4=(0-2+0+4)=2,a5+a6+a7+a8=(0-6+0+8)=2,,…,a2009+a2010+a2011+a2012=(0-2010+0+2012)=2, S2012=a1+a2+a3+a4+…+a2012+ a2013,=(0-2+0+4)+(0-6+0+8)+…+(0-2010+0+2012)+0,=2×503=1006,故选A
考点:数列的求和
点评:解决的关键是根据其周期性来得到数列的求和的规律性的结论,属于基础题。

练习册系列答案
相关题目
数列 的通项公式是
的通项公式是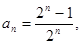 其前
其前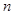 项和为
项和为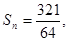 则项数
则项数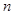 等于
等于
| A.6 | B.9 | C.10 | D.13 |
已知数列 的通项公式为
的通项公式为 ,那么满足
,那么满足 的整数
的整数 ( )
( )
| A.有3个 | B.有2个 | C.有1个 | D.不存在 |
已知数列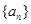 的前
的前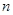 项和为
项和为 ,
,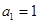 ,
,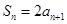 ,,则
,,则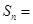 ( )
( )
A.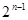 | B.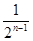 | C.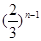 | D.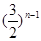 |
定义:称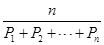 为
为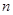 个正数
个正数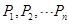 的“均倒数”.若数列
的“均倒数”.若数列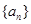 的前
的前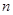 项的“均倒数”为
项的“均倒数”为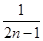 ,则数列
,则数列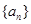 的通项公式为( )
的通项公式为( )
A.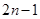 | B. | C. | D.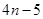 |
设数列 是等差数列,且
是等差数列,且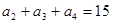 ,则这个数列的前5项和
,则这个数列的前5项和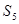 =
=
| A. 10 | B. 15 | C. 20 | D. 25 |
等比数列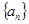 各项为正,
各项为正,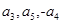 成等差数列.
成等差数列.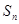 为
为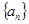 的前n项和,则
的前n项和,则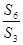 =( )
=( )
| A.2 | B.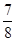 | C.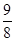 | D.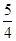 |
数列 满足
满足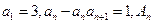 表示
表示 前n项之积,则
前n项之积,则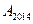 的值为( )
的值为( )
| A.-3 |
B.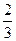 |
| C.3 |
D.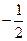 |
 是首项为3,公差为1的等差数列,数列
是首项为3,公差为1的等差数列,数列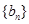 是首项为
是首项为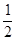 ,公比也为
,公比也为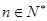 ,那么数列
,那么数列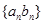 的前
的前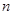 项和
项和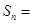 ______.
______.