题目内容
等比数列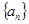 各项为正,
各项为正,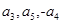 成等差数列.
成等差数列.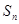 为
为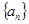 的前n项和,则
的前n项和,则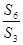 =( )
=( )
| A.2 | B.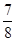 | C.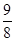 | D.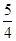 |
C
解析试题分析:设{an}的公比为q(q≠0,q≠1),利用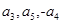 成等差数列结合通项公式,可得
成等差数列结合通项公式,可得 ,由此即可求得数列{an}的公比,进而求出数列的前n项和公式,可得答案
,由此即可求得数列{an}的公比,进而求出数列的前n项和公式,可得答案
设{an}的公比为q(q>0,q≠1)
∵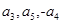 成等差数列,∴
成等差数列,∴
∵a1≠0,q≠0,∴2q2+q-1=0, ,故
,故 ,故选C.
,故选C.
考点:等比数列的公式运用
点评:解决该试题的关键是对于数列公式的熟练表示和运用,属于基础题 。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
阅读如图程序框图,若输入的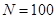 ,则输出的结果是( )
,则输出的结果是( )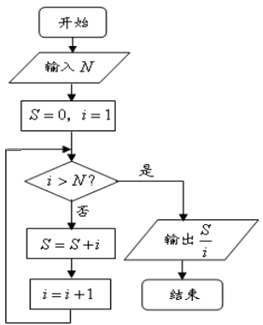
A.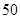 | B.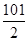 | C.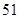 | D.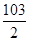 |
数列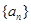 的通项公式
的通项公式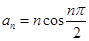 ,其前
,其前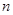 项和为
项和为 ,则
,则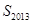 等于( )
等于( )
| A.1006 | B.2012 | C.503 | D.0 |
已知数列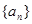 满足
满足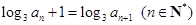 ,且
,且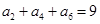 ,则
,则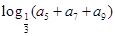 的值是( )
的值是( )
A.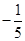 | B.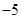 | C.5 | D.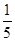 |
在数列{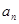 }中,若对任意的n均有
}中,若对任意的n均有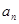 +
+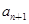 +
+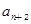 为定值
为定值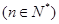 ,且
,且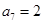 ,
,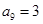 ,
,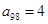 则数列
则数列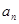 的前100项的和S100= ( )
的前100项的和S100= ( )
| A.132 | B.299 | C.68 | D.99 |
设等比数列 的公比为
的公比为 ,前n项和为
,前n项和为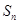 ,若
,若 ,
,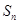 ,
,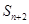 成等差数列,则公比
成等差数列,则公比 为( ).
为( ).
A.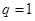 | B. | C. 或 或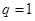 | D. 或 或 |
已知数列{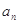 }满足
}满足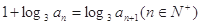 ,且
,且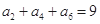 ,则
,则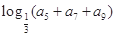 的值是 ( )
的值是 ( )
A.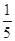 | B.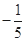 | C.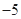 | D.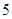 |
若数列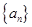 的通项公式是
的通项公式是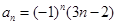 ,则
,则 ( )
( )
| A.15 | B.12 | C.-12 | D.-15 |
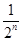 ,n∈N?,则a3=________.
,n∈N?,则a3=________.