题目内容
已知关于x的一元二次方程x2-ax+2a-3=0,求使方程有两个大于零的实数根的充要条件.
解:设x1,x2是方程的两根,则原方程的两个根都大于0的等价条件是
即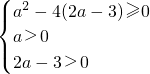
解得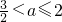 或a≥6
或a≥6
∴a的取值范围是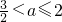 或a≥6.
或a≥6.
分析:原方程的两个根都大于0的等价条件是方程的判别式大于等于0,两根之和大于0,两根之积大于0,从而可建立不等式组,进而可求得使方程有两个大于零的实数根的充要条件
点评:本题考查的重点是方程根的研究,解题的关键是利用韦达定理,建立不等关系.

即
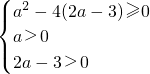
解得
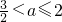 或a≥6
或a≥6∴a的取值范围是
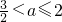 或a≥6.
或a≥6.分析:原方程的两个根都大于0的等价条件是方程的判别式大于等于0,两根之和大于0,两根之积大于0,从而可建立不等式组,进而可求得使方程有两个大于零的实数根的充要条件
点评:本题考查的重点是方程根的研究,解题的关键是利用韦达定理,建立不等关系.

练习册系列答案
相关题目