题目内容
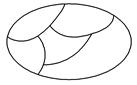
某城市在中心广场建造一个花圃,花圃分为6个部分(如图).现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有多少种(用数字作答).


120
方法一:从题意来看,6部分种4种颜色的花,又从图形看,知必有2组同颜色的花,从同颜色的花入手分类求解.
(1)2与5同色,则3,6也同色或4,6也同色,所以共有N1=4×3×2×2×1=48(种);
(2)3与5同色,则2,4或4,6同色,所以共有N2=4×3×2×2×1=48(种);
(3)2与4且3与6同色,所以共有N3=4×3×2×1=24(种).
所以,共有N=N1+N2+N3=48+48+24=120(种).
方法二:记颜色为A,B,C,D四色,先安排1,2,3有4×3×2种不同的栽法,不妨设1,2,3已分别栽种A,B,C,则4,5,6栽种方法共5种,由以下树状图清晰可见.
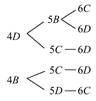
根据分步乘法计数原理,不同的栽种方法有N=4×3×2×5=120(种).
(1)2与5同色,则3,6也同色或4,6也同色,所以共有N1=4×3×2×2×1=48(种);
(2)3与5同色,则2,4或4,6同色,所以共有N2=4×3×2×2×1=48(种);
(3)2与4且3与6同色,所以共有N3=4×3×2×1=24(种).
所以,共有N=N1+N2+N3=48+48+24=120(种).
方法二:记颜色为A,B,C,D四色,先安排1,2,3有4×3×2种不同的栽法,不妨设1,2,3已分别栽种A,B,C,则4,5,6栽种方法共5种,由以下树状图清晰可见.

根据分步乘法计数原理,不同的栽种方法有N=4×3×2×5=120(种).

练习册系列答案
相关题目
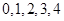 中任取四个数字组成无重复数字的四位数,其中偶数的个数是 (用数字作答).
中任取四个数字组成无重复数字的四位数,其中偶数的个数是 (用数字作答).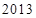 个数字是 .
个数字是 .