题目内容
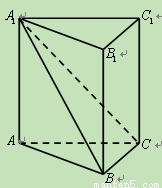
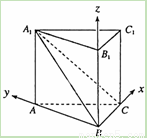
(本小题满分12分)如图,在直三棱柱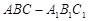 中,平面
中,平面 侧面
侧面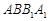 .
.
(Ⅰ)求证: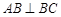 ;
;
(Ⅱ)若直线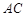 与平面
与平面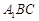 所成角是
所成角是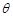 ,锐二面角
,锐二面角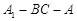 的平面角是
的平面角是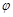 ,试判断
,试判断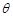 与
与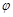 的大小关系,并予以证明.
的大小关系,并予以证明.
本小题满分12分)
(I)
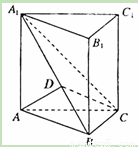
证明:如图,过点A在平面A1ABB1内作AD⊥A1B于D,
则由平面A1BC⊥侧面A1ABB1于A1B,
得AD⊥平面A1BC, ………………(2分)
又BC 平面A1BC,∴AD⊥BC.
平面A1BC,∴AD⊥BC.
在直三棱柱ABC—A1B1C1中,
AA1⊥底面ABC,∴AA1⊥BC. ………………(4分)
又AA1∩AD=A,从而BC⊥侧面A1ABB1,
又AB 侧面A1ABB1,故AB⊥BC;…………(6分)
侧面A1ABB1,故AB⊥BC;…………(6分)
(II)
方法1:连接CD,则由(I)知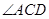 是直线AC与平面A1BC所成的角,
是直线AC与平面A1BC所成的角,
………………(8分)
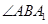 是二面角A1—BC—A的平面角,即
是二面角A1—BC—A的平面角,即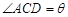 ,
,
………………(10分)
在Rt△ADC中, 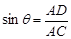 ,在Rt△ADB中,
,在Rt△ADB中,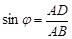 ,
,
由AC 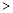 AB,得
AB,得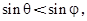 又
又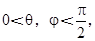 所以
所以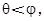
………………(12分)
方法2:设AA1=a,AB=b,BC=c,由(I)知,以点B为坐标原点,以BC、BA、BB1所在
的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则 B(0,0,0), A(0,b,0),C(c,0,0),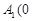 ,b,a),
,b,a),
∴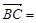 (c,0,0),
(c,0,0),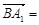 ( 0,b,a),…………(7分)
( 0,b,a),…………(7分)
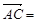 ( c,-b,0),设平面A1BC的一个
( c,-b,0),设平面A1BC的一个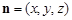 ,
,
由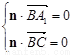 ,得
,得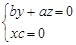 ,取
,取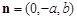 ,
……………(9分)
,
……………(9分)
∴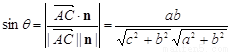 ,
,
∵平面ABC的法向量为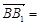 ( 0,0,a),∵二面角A1—BC—A的平面角是锐角,
( 0,0,a),∵二面角A1—BC—A的平面角是锐角,
∴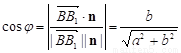 ,
,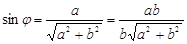
……………(10分)
∵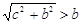 ,∴
,∴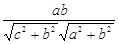
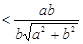 ,
,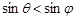 ,
,
∵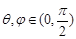 ,∴
,∴ .
………………(12分)
.
………………(12分)
【解析】略
