题目内容
已知函数f(x)=log2x(x>1),若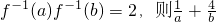 的最小值为
的最小值为
- A.4
- B.5
- C.8
- D.9
D
分析:先求出f(x)的反函数f-1(x)=2x(x>0)根据条件可得出a+b=1而 ,
,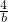 的积不是定值则可利用“1”的代换即
的积不是定值则可利用“1”的代换即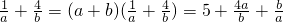 从而实现了“积定和最小”然后直接利用基本不等式求解即可.
从而实现了“积定和最小”然后直接利用基本不等式求解即可.
解答:∵f(x)=log2x(x>1)
∴f-1(x)=2x(x>0)
∴f-1(a)f-1(b)=2a+b=2
∴a+b=1
∴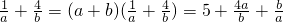
∵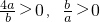
∴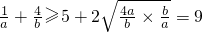 (当且仅当
(当且仅当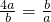 即a=
即a= ,b=
,b= 时取等号)
时取等号)
故选D
点评:本题主要考查了利用基本不等式求最值.解题的关键是要注意“一正”,“二定”即凑成“和定”或:“积定”的形式否者的话要利用一些常用的变形比如本题中的“1”的代换,“三相等”!
分析:先求出f(x)的反函数f-1(x)=2x(x>0)根据条件可得出a+b=1而
 ,
,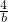 的积不是定值则可利用“1”的代换即
的积不是定值则可利用“1”的代换即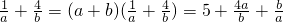 从而实现了“积定和最小”然后直接利用基本不等式求解即可.
从而实现了“积定和最小”然后直接利用基本不等式求解即可.解答:∵f(x)=log2x(x>1)
∴f-1(x)=2x(x>0)
∴f-1(a)f-1(b)=2a+b=2
∴a+b=1
∴
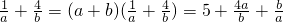
∵
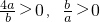
∴
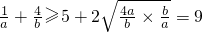 (当且仅当
(当且仅当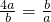 即a=
即a= ,b=
,b= 时取等号)
时取等号)故选D
点评:本题主要考查了利用基本不等式求最值.解题的关键是要注意“一正”,“二定”即凑成“和定”或:“积定”的形式否者的话要利用一些常用的变形比如本题中的“1”的代换,“三相等”!

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目