题目内容
已知等差数列 的公差为2,若
的公差为2,若 成等比数列,则
成等比数列,则 =( )
=( )
 的公差为2,若
的公差为2,若 成等比数列,则
成等比数列,则 =( )
=( )A. | B. | C. | D. |
B
试题分析:直接利用a1,a3,a4成等比数列求出首项和公差的关系,再把公差代入即可求出a1.解:因为a1,a3,a4成等比数列,所以有a32=a1•a4⇒(a1+2d)2=a1•(a1+3d)⇒a1•d=-4d2,又因为d=2,所以a1=-8.故答案为:B
点评:本题考查等差数列与等比数列的基础知识,考查方程思想在解决数列问题中的应用.在等差数列、等比数列问题中基本量是解题的关键,一般是根据已知条件把基本量求出来,然后在解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
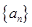 中,
中,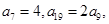
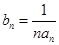 ,求数列
,求数列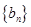 的前n项和
的前n项和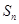 .
. 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,公差
,公差 ,
,  ,则
,则 ( )
( )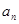 }的前n项和
}的前n项和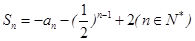 ,数列{
,数列{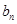 }满足
}满足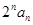 .
.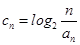 ,数列{
,数列{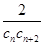 }的前n项和为Tn,求满足
}的前n项和为Tn,求满足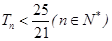 的n的最大值.
的n的最大值.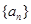 的前n项和为
的前n项和为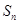 ,点
,点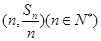 均在函数y=-x+12的图像上.
均在函数y=-x+12的图像上.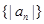 的前n项的和.
的前n项的和.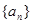 是各项都为正数的等比数列,
是各项都为正数的等比数列, 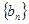 是等差数列,且
是等差数列,且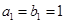 ,
,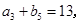
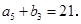
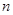 项和为
项和为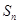 ,求数列
,求数列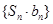 的前
的前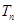 .
.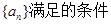 ,
,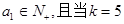 时,输出的
时,输出的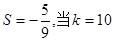 时,输出的
时,输出的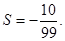 (其中d为公差)
(其中d为公差)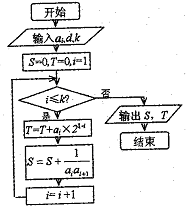
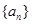 的通项公式;
的通项公式;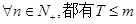 成立?若存在,求出m的值,若不存在,请说明理由。
成立?若存在,求出m的值,若不存在,请说明理由。