题目内容
O是平面上一点,A、B、C是平面上不共线三点,动点P满足
=
+λ(
+
),λ=
时,则
•(
+
)的值为
| OP |
| OA |
| AB |
| AC |
| 1 |
| 2 |
| PA |
| PB |
| PC |
0
0
.分析:通过已知的向量关系,求出
,说明P的位置,推出
+
=0,然后求解结果即可.
| AP |
| PB |
| PC |
解答: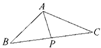 解:由
解:由
=
+λ(
+
),λ=
,
得
=
(
+
),
即P为△ABC中BC边的中点.
∴
+
=
.
∴
•(
+
)=
•
=0.
故答案为:0.
 解:由
解:由| OP |
| OA |
| AB |
| AC |
| 1 |
| 2 |
得
| AP |
| 1 |
| 2 |
| AB |
| AC |
即P为△ABC中BC边的中点.
∴
| PB |
| PC |
| 0 |
∴
| PA |
| PB |
| PC |
| PA |
| 0 |
故答案为:0.
点评:本题考查向量的坐标运算,向量的几何意义,考查计算能力.

练习册系列答案
相关题目
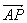 ],λ∈[0,+∞]则P的轨迹一定通过△ABC的( )
],λ∈[0,+∞]则P的轨迹一定通过△ABC的( )