题目内容
O是平面上一点，A，B，C是平面上不共线三点，动点P满足| OP |
| OA |
| AB |
| AC |
| 1 |
| 2 |
| 1 |
| 2 |
| AP |
| PA |
| PB |
| PC |
分析：设BC的中点为D，由题意可得AD=2，且点P在线段AD上，从而得到
•(
+
)=
•2
=2x（2-x）cos180°=2（x-1）2-2，利用二次函数的性质得到其最小值．
| PA |
| PB |
| PC |
| PA |
| PD |
解答：解：∵
=
+λ(
+
)，(λ∈[0，
])，设BC的中点为D，∴
=λ（
+
）=λ
，
且点P在线段AD上，当λ=
时，|
|=2=|
|，即 P和D重合时，AD=2．
•(
+
）=
•2
，设PA=x，则PD=2-x，x∈[0，2]，
∴
•2
=2x（2-x）cos180°=2（x-1）2-2≥-2，故
•(
+
)的最小值等于-2，
故答案为-2．
| OP |
| OA |
| AB |
| AC |
| 1 |
| 2 |
| AP |
| AB |
| AC |
| AD |
且点P在线段AD上，当λ=
| 1 |
| 2 |
| AP |
| AD |
| PA |
| PB |
| PC |
| PA |
| PD |
∴
| PA |
| PD |
| PA |
| PB |
| PC |
故答案为-2．
点评：本题考查两个向量的数量积的定义，两个向量的加减法的法则，以及其几何意义，得到
•(
+
)=
•2
=2x（2-x）cos180°，是解题的关键．
| PA |
| PB |
| PC |
| PA |
| PD |
练习册系列答案
科学实验活动册系列答案
相关题目
=
+λ[
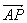],λ∈[0，+∞]则P的轨迹一定通过△ABC的（ ）